已知椭圆的两个焦点为F1.F2.A为椭圆上一点.AF1⊥AF2.∠AF2F1=60°.求该椭圆的离心率．题目和参考答案——青夏教育精英家教网—

题目内容

已知椭圆的两个焦点为F₁，F₂，A为椭圆上一点，AF₁⊥AF₂，∠AF₂F₁=60°，求该椭圆的离心率．

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：由已知中AF₁⊥AF₂，∠AF₂F₁=60°，可得2a=AF₁+AF₂=（

+1）c，进而可得椭圆的离心率．

解答： 解：∵椭圆的两个焦点为F₁，F₂，A为椭圆上一点，AF₁⊥AF₂，∠AF₂F₁=60°，
则AF₁=sin60°F₁F₂=

c，AF₂=cos60°F₁F₂=c，
即2a=AF₁+AF₂=（

+1）c，
故椭圆的离心率e=

(

+1)c

-1

点评：本题考查的知识点是椭圆的简单性质，难度不大，属于基础题．

练习册系列答案

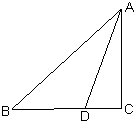如图，在Rt△ABC（C为直角）中，D为BC边上的一个三等分点（靠近点C），则tan∠BAD的最大值为

已知函数f（x）=sin（2x+φ），其中φ为实数，且f（x）≤f（

已知M（3，m）在抛物线C：y²=2px（p＞0）上，F为焦点，|MF|=5．
（1）求m的值和抛物线c的方程；
（2）求抛物线C上的点P到直线l：x-y+5=0的距离的最小值．

设函数f（x）=

，[x]表示不超过x的最大整数，则函数y=[f（x））]的值域集合

．

某校高一、高二两个年级进行乒乓球对抗赛，每个年级选出3名学生组成代表队，比赛规则是：
①按“单打、双打、单打”顺序进行三盘比赛；
②代表队中每名队员至少参加一盘比赛，但不能参加两盘单打比赛．若每盘比赛中高一、高二获胜的概率分别为

，

．
（1）按比赛规则，高一年级代表队可以派出多少种不同的出场阵容？
（2）若单打获胜得2分，双打获胜得3分，求高一年级得分ξ的概率发布列和数学期望．

已知a，b∈R，

3+i

1-i

=a+bi（i为虚数单位），则a+b=（　　）

试题分类