题目内容
已知x>0,y>0,x,a,b,y成等差数列,x,c,d,y成等比数列,求
的最小值.
| (a+b)2 |
| cd |
考点:等比数列的性质,等差数列的性质
专题:计算题,等差数列与等比数列
分析:首先由等差数列和等比数列的性质可得a+b=x+y,cd=xy,然后利用均值不等式求解即可.
解答:
解:∵x,a,b,y成等差数列,x,c,d,y成等比数列,
根据等差数列和等比数列的性质可知:a+b=x+y,cd=xy,
∴
=
≥
=4
当且仅当x=y时取“=”,
故
的最小值为4.
根据等差数列和等比数列的性质可知:a+b=x+y,cd=xy,
∴
| (a+b)2 |
| cd |
| (x+y)2 |
| xy |
(2
| ||
| xy |
当且仅当x=y时取“=”,
故
| (a+b)2 |
| cd |
点评:本题考查等差数列和等比数列的性质,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
在钝角△ABC中,a=1,b=2,则最大边c的取值范围是( )
| A、1<c<3 | ||
| B、2<c<3 | ||
C、
| ||
D、2
|
函数y=2|X-1|的图象为( )
A、 |
B、 |
C、 |
D、 |
已知向量
=(1,2),
=(2,3),则λ<-4是向量
=λ
+
与向量
=(3,-1)夹角钝角的( )
| a |
| b |
| m |
| a |
| b |
| n |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
已知集合M={5,6,7},N={5,7,8},则( )
| A、M⊆N |
| B、M?N |
| C、M∩N={5,7} |
| D、M∪N={6,7,8} |
 随机抽取某产品n件,测得其长度分别为x1,x2,…xn,则图所示的程序框图输出的s表示的样本的数字特征是
随机抽取某产品n件,测得其长度分别为x1,x2,…xn,则图所示的程序框图输出的s表示的样本的数字特征是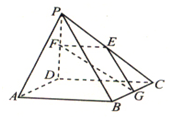 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.