题目内容
7.如果实数x,y 满足条件 $\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$,则z=$\frac{y}{x}$的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 作出平面区域,则 $\frac{y}{x}$表示过原点和平面区域内一点的直线斜率.
解答  解:作出 $\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$的平面区域如图所示:
解:作出 $\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$的平面区域如图所示:
由平面区域可知当直线y=kx过A点时,斜率最大.
解方程组得$\left\{\begin{array}{l}{x-y+1=0}\\{2x+y-2=0}\end{array}\right.$得A($\frac{1}{3}$,$\frac{4}{3}$).
∴z的最大值为$\frac{\frac{4}{3}}{\frac{1}{3}}$=4.
故选:B.
点评 本题考查了简单的线性规划,作出平面区域,找到z=$\frac{y}{x}$的几何意义是关键,属于中档题.

练习册系列答案
相关题目
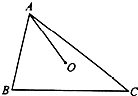 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28. 在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.
在直三棱柱ABC-A1B1C1 中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.