题目内容
12.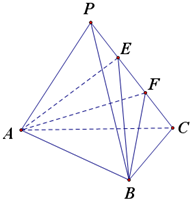 在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.
在三棱锥P-ABC中,PA=PB=PC=3,AB=$\sqrt{6}$,BC=$\sqrt{3}$,AB⊥BC,E,F为PC的三等分点.(1)求证:面PAC⊥面ABC.
(2)求:VA-BEF.
分析 (1)取AC中点H,连接PH和BH,由AB⊥BC,即∠ABC=90°,得AH=CH=BH,又PA=PB=PC,可得△PAH≌△PCH≌△PBH,得到PH⊥AC,说明PH⊥面ABC,再由面面垂直的判定得答案;
(2)把VA-BEF转化为VB-AEF的体积,进一步转化为$\frac{1}{9}{V}_{P-ABC}$求解.
解答 证明:(1)取AC中点H,连接PH和BH,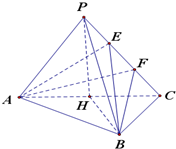
∵AB⊥BC,
∴∠ABC=90°,
∴AH=CH=BH,又PA=PB=PC,
∴△PAH≌△PCH≌△PBH,
在△PAC中PH⊥AC,
∴PH⊥面ABC,
又PH?面PAC,面PAC⊥面ABC;
解:(2)△ABC中$AB=\sqrt{6},BC=\sqrt{3}$,则AC=3,高$h=\frac{{\sqrt{6}•\sqrt{3}}}{3}=\sqrt{2}$,
∴VA-BEF=${V_{B-AEF}}=\frac{1}{3}{S_{△AEF}}•h=\frac{1}{9}{S_{△PAC}}•h$=$\frac{1}{9}×\frac{{\sqrt{3}}}{4}×{3^2}×\sqrt{2}=\frac{{\sqrt{6}}}{4}$.
点评 本题考查平面与平面垂直的判定,考查利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设函数f(x)=sin(2x+φ)+cos(2x+φ)(|φ|<$\frac{π}{2}$)为偶函数,则φ=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
3.已知y=f(x)为R上的连续可导的奇函数,当x>0时f′(x)+$\frac{f(x)}{x}$<0,则g(x)=f(x)+$\frac{2}{x}$的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
1.正三角形ABC的边长为1,设$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{BC}$=$\vec b$,$\overrightarrow{AC}$=$\vec c$,那么$\vec a$•$\vec b$+$\vec b$•$\vec c$+$\vec c$•$\vec a$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
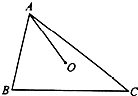 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.