题目内容
9.函数f(x)=$\sqrt{1-x}$-$\sqrt{x}$的定义域为( )| A. | [0,1] | B. | (0,1] | C. | (0,1) | D. | (-1,0) |
分析 根据函数f(x)的解析式,列出使解析式有意义的不等式组,从而求出函数的定义域.
解答 解:∵函数f(x)=$\sqrt{1-x}$-$\sqrt{x}$,
∴$\left\{\begin{array}{l}{1-x≥0}\\{x≥0}\end{array}\right.$,
解得0≤x≤1,
∴函数f(x)的定义域为[0,1].
故选:A.
点评 本题考查了根据函数的解析式求定义域的应用问题,是基础题目.

练习册系列答案
相关题目
1.正三角形ABC的边长为1,设$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{BC}$=$\vec b$,$\overrightarrow{AC}$=$\vec c$,那么$\vec a$•$\vec b$+$\vec b$•$\vec c$+$\vec c$•$\vec a$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
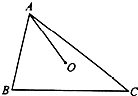 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.
如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是28.