题目内容

在等比数列{an}中，2a3-a2a4=0，若{bn}为等差数列，且b3=a3，则数列{bn}的前5项和等于
 
．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据2a3-a2a4=0求出a3=2，然后根据等差数列的前n项和公式即可得到结论．
解答： 解：在等比数列{an}中，
由2a3-a2a4=0，得2a3-（a3）2=0，
即a3=2，
{bn}为等差数列，且b3=a3，
∴b3=a3=2，
则数列{bn}的前5项和等于
5(a1+a5)
2
=
5×2a3
2
=5×2=10，
故答案为：10．
点评：本题主要等差数列和等比数列的通项公式的应用，根据等差数列和等比数列的性质是解决本题的关键．
练习册系列答案
相关题目
请设计算法框图，要求输入自变量x的值，输出函数f（x）=
-x+1，x≥0
x+3，x＜0
的值．
已知函数f（x）=ax-2-2（a＞0且a≠1）的图象恒过定点A（m，n），则不等式组
mx+ny+2≥0
8x-y-4≤0
x≥0，y≥0
所表示的平面区域的面积是
 
．
在锐角△ABC中，AC=BC=2，
CO
=x
CA
+y
CB
，（其中x+y=1），函数f（λ）=|
CA
-λ
CB
|的最小值为
3
，则|
CO
|的最小值为
 
．
在极坐标系中，过点（3，
π
3
）且垂直于极轴的直线方程的极坐标方程是
 
（请选择正确标号填空）．（1）ρ=
3
2
sinθ；（2）ρ=
3
2
cosθ；（3）ρsinθ=
3
2
；（4）ρcosθ=
3
2
．
设实数x，y满足
y≤x
x+y≤1
y≥-1
，则2x-y的最大值是
 
．
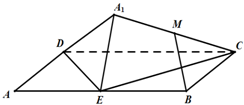如图，矩形ABCD中，AB=2BC=4，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，正确的命题是
 
．
①|BM|是定值；
②点M在圆上运动；
③一定存在某个位置，使DE⊥A1C；
④一定存在某个位置，使MB∥平面A1DE．
给出下列四个命题：
①“M＞N”是“log2M＞log2N”的充要条件；
②已知A、B是双曲线
x2
a2
-
y2
b2
=1实轴的两个端点，M，N是双曲线上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2，且k1k2≠0．若|k1|+|k2|的最小值为2，则双曲线的离心率e=
2
；
③取一根长度为3m的绳子，拉直后在任意位置剪断，那么剪得两段的长都不小于1m的概率是
1
3
；
④一个圆形纸片，圆心为O，F为圆内一定点，M是圆周上一动点，把纸片折叠使M与F重合，然后抹平纸片，折痕为CD，设CD与OM交于P，则P的轨迹是椭圆．
其中真命题的序号是
 
．（填上所有真命题的序号）
若双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线与抛物线x2=4y的准线所围成的三角形面积为2，则该双曲线的离心率为（　　）
A、
5
2
B、
2
C、
3
D、
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网