题目内容
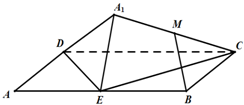如图，矩形ABCD中，AB=2BC=4，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，正确的命题是①|BM|是定值；
②点M在圆上运动；
③一定存在某个位置，使DE⊥A1C；
④一定存在某个位置，使MB∥平面A1DE．
考点：平面与平面之间的位置关系
专题：综合题,空间位置关系与距离
分析：取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得④正确；由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，M是在以B为圆心，MB为半径的圆上，可得①②正确．A1C在平面ABCD中的射影为AC，AC与DE不垂直，可得③不正确．
解答：
解：取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故④正确
由∠A1DE=∠MNB，MN=
A1D=定值，NB=DE=定值，
由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，故①正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故②正确，
∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，
∴存在某个位置，使DE⊥A1C不正确，故③不正确．
故答案为：①②④．
由∠A1DE=∠MNB，MN=
| 1 |
| 2 |
由余弦定理可得MB2=MN2+NB2-2MN•NB•cos∠MNB，所以MB是定值，故①正确．
∵B是定点，∴M是在以B为圆心，MB为半径的圆上，故②正确，
∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，
∴存在某个位置，使DE⊥A1C不正确，故③不正确．
故答案为：①②④．
点评：掌握线面、面面平行与垂直的判定和性质定理及线面角、二面角的定义及求法是解题的关键．
练习册系列答案
相关题目
某学校为了了解学生的日平均睡眠时间（单位：h），随机选择了n名同学进行调查．下表是这n名同学的日睡眠时间的频率分布表．
如图，⊙O中，直径AB和弦DE互相垂直，C是DE延长线上一点，连结BC与圆O交于F，若∠DBC=下列命题是真命题的是（ ）
| A、?x∈R，x2+2＞2 |
| B、?x0∈Q，x02=3 |
| C、?x∈N，x2≥1 |
| D、?x0∈Z，x03＜1 |