题目内容
给出下列四个命题:
①“M>N”是“log2M>log2N”的充要条件;
②已知A、B是双曲线
-
=1实轴的两个端点,M,N是双曲线上关于x轴对称的两点,直线AM,BN的斜率分别为k1,k2,且k1k2≠0.若|k1|+|k2|的最小值为2,则双曲线的离心率e=
;
③取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是
;
④一个圆形纸片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆.
其中真命题的序号是 .(填上所有真命题的序号)
①“M>N”是“log2M>log2N”的充要条件;
②已知A、B是双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
③取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率是
| 1 |
| 3 |
④一个圆形纸片,圆心为O,F为圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于P,则P的轨迹是椭圆.
其中真命题的序号是
考点:命题的真假判断与应用
专题:综合题
分析:①通过举反例判定命题不成立;
②根据题意,求出|k1|+|k2|的最小值为2时,a、b的关系,从而求出双曲线的离心率e;
③画出图形,求出剪得两段的长都不小于1m的概率P;
④画出图形,根据题意,求出点P满足的关系式,结合椭圆的定义,得出P点的轨迹.
②根据题意,求出|k1|+|k2|的最小值为2时,a、b的关系,从而求出双曲线的离心率e;
③画出图形,求出剪得两段的长都不小于1m的概率P;
④画出图形,根据题意,求出点P满足的关系式,结合椭圆的定义,得出P点的轨迹.
解答:
解:①当0>M>N时,log2M、log2N无意义,当log2M>log2N时,M>N,应是必要不充分条件,∴命题错误;
②根据题意,设A(-a,0),B(a,0),M(m,n),则N(m,-n);
∴
-
=1(a>0,b>0),
∴n2=
;
∴k1=
,k2=
,
∴|
|+|
|≥2
=2•
=2,
∴b=a,
∴双曲线的离心率e=
;命题正确;
③如图所示, ;
;
在中间的1m处剪开,剪得两段的长都不小于1m,概率是P=
=
,∴命题正确;
④如图所示, 由题意知,CD是线段MF的垂直平分线,
由题意知,CD是线段MF的垂直平分线,
∴|MP|=|FP|,
∴|FP|+|PO|=|PM|+|PO|=|MO|(定值),
又显然|MO|>|FO|,
∴根据椭圆的定义知点P轨迹是以F、O两点为焦点的椭圆;∴命题正确;
以上正确的命题有3个,是②③④;
故答案为:②③④.
②根据题意,设A(-a,0),B(a,0),M(m,n),则N(m,-n);
∴
| m2 |
| a2 |
| n2 |
| b2 |
∴n2=
| (m2-a2)b2 |
| a2 |
∴k1=
| n |
| m+a |
| -n |
| m-a |
∴|
| n |
| m+a |
| -n |
| m-a |
|
| b |
| a |
∴b=a,
∴双曲线的离心率e=
| 2 |
③如图所示,
 ;
;在中间的1m处剪开,剪得两段的长都不小于1m,概率是P=
| 3-1-1 |
| 3 |
| 1 |
| 3 |
④如图所示,
 由题意知,CD是线段MF的垂直平分线,
由题意知,CD是线段MF的垂直平分线,∴|MP|=|FP|,
∴|FP|+|PO|=|PM|+|PO|=|MO|(定值),
又显然|MO|>|FO|,
∴根据椭圆的定义知点P轨迹是以F、O两点为焦点的椭圆;∴命题正确;
以上正确的命题有3个,是②③④;
故答案为:②③④.
点评:本题考查了充要条件、双曲线、概率以及椭圆的有关问题,是综合题目.

练习册系列答案
相关题目
已知i是虚数单位,若复数z满足i=
,则z=( )
| 1-i |
| z |
| A、-1-i | B、-1+i |
| C、1-i | D、1+i |
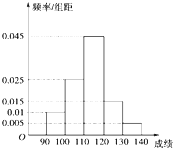 某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人. 如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连结BC与圆O交于F,若∠DBC=
如图,⊙O中,直径AB和弦DE互相垂直,C是DE延长线上一点,连结BC与圆O交于F,若∠DBC=