题目内容
7.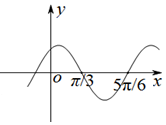 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
分析 根据函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象过($\frac{5π}{6}$,0),$\frac{1}{2}T=\frac{5π}{6}-\frac{π}{3}$即可求解ω,φ可得f(x)的解析式,通过图象向左平移$\frac{π}{6}$个单位,得到g(x)的解析式.
解答 解:由图象可知,$\frac{1}{2}T=\frac{5π}{6}-\frac{π}{3}$,可得T=π,∴$ω=\frac{2π}{T}$=2.、
得函数f(x)=sin(2x+φ)
又f(x)图象过($\frac{π}{3}$,0),可得sin(2×$\frac{π}{3}$+φ)=0,
∵0<φ<π,
∴$\frac{2π}{3}$+φ=π,
可得φ=$\frac{π}{3}$.
∴函数f(x)=sin(2x+$\frac{π}{3}$)
图象向左平移$\frac{π}{6}$个单位,得sin[(2x+$\frac{π}{6}$)+$\frac{π}{3}$]=sin(2x+$\frac{2π}{3}$)=g(x).
则函数g(x)的解析式为g(x)=sin(2x+$\frac{2π}{3}$).
故选D.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
19.设Sn是等差数列{an}的前n项和,且a11=S13=13,则a9=( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
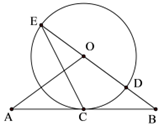 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.