题目内容
19.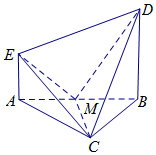 如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.
如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.(Ⅰ)求证:CM⊥EM;
(Ⅱ)若直线DM与平面ABC所成角的正切值为2,求二面角B-CD-E的余弦值.
分析 (Ⅰ)证明CM⊥AB,CM⊥EA.推出CM⊥平面EAM.然后证明CM⊥EM.
(Ⅱ)以点M为坐标原点,MC所在直线为x轴,MB所在直线为y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系M-xyz.说明∠DMB为直线DM与平面ABC所成角.设AC=2,求出相关点的坐标,求出平面BCD与平面CDE的法向量,利用空间向量的数量积求解即可.
解答 解:(Ⅰ)因为△ABC是等边三角形,M是AB的中点,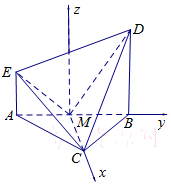
所以CM⊥AB.…(1分)
因为EA⊥平面ABC,CM?平面ABC,
所以CM⊥EA.…(2分)
因为AM∩EA=A,
所以CM⊥平面EAM.…(3分)
因为EM?平面EAM,
所以CM⊥EM.…(4分)
(Ⅱ)以点M为坐标原点,MC所在直线为x轴,
MB所在直线为y轴,过M且与直线BD平行的直线为z轴,
建立空间直角坐标系M-xyz.
因为DB⊥平面ABC,
所以∠DMB为直线DM与平面ABC所成角.…(5分)
由题意得tan∠DMB=$\frac{BD}{MB}$=2,即BD=2MB,…(6分)
从而BD=AC.
不妨设AC=2,又AC-2AE,则CM=$\sqrt{3}$,AE=1.…(7分)
故B(0,1,0),C($\sqrt{3}$,0,0),D(0,1,2),E(0,-1,1).…(8分)
于是$\overrightarrow{BC}$=($\sqrt{3}$,-1,0),$\overrightarrow{BD}$=(0,0,2),$\overrightarrow{CE}$=(-$\sqrt{3}$,-1,1),$\overrightarrow{CD}$=(-$\sqrt{3}$,1,2),
设平面BCD与平面CDE的法向量分别为$\overrightarrow{m}=({x}_{1}{y}_{1},{z}_{1})$,$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$,
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=0}\\{\overrightarrow{m}•\overrightarrow{BD}=0}\end{array}\right.$可得$\left\{\begin{array}{l}{\sqrt{3}{x}_{1}-{y}_{1}=0}\\{2{z}_{1}=0}\end{array}\right.$ 令x1=1,得y1=$\sqrt{3}$,
所以$\overrightarrow{m}$=(1,$\sqrt{3}$,0).…(9分)
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=0}\\{\overrightarrow{n}•\overrightarrow{CD}=0}\end{array}\right.$ 得$\left\{\begin{array}{l}{-\sqrt{3}{x}_{2}-{y}_{2}+{z}_{2}=0}\\{-\sqrt{3}{x}_{2}+{y}_{2}+2{z}_{2}=0}\end{array}\right.$,令x2=1,得y2=$-\frac{\sqrt{3}}{3}$,z2=$\frac{2\sqrt{3}}{3}$.
所以$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$).…(10分)
所以cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=0.…(11分)
所以二面角B-CD-E的余弦值为0.…(12分)
点评 本题综合考查了直线与平面垂直的判定定理及其性质定理,面面垂直的性质定理,二面角的求法、考查了推理能力、辅助线的作法,属于中档题.

| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |