Question

如图1，△ABC是正三角形，△ABD是等腰直角三角形，AB=BD=2．将△ABD沿边AB折起，使得△ABD与△ABC成30°的二面角D-AB-C，如图2，在二面角D-AB-C中．

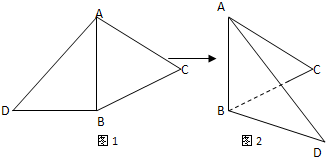
（1）求D、C之间的距离；
（2）求CD与面ABC所成的角的大小．

Answer 1

考点：直线与平面所成的角,点、线、面间的距离计算

专题：空间位置关系与距离

分析：（1）依题意建立空间直角坐标系使得△ABC在yoz平面上，由已知条件分别求出点C和点D的空间坐标，利用空间两点间的距离公式能求出D、C之间的距离．
（2）由题设条件求出面ABC的一个法向量和向量

CD

，利用向量法能求出CD与平面ABC所成的角．

解答： 解：（1）依题意，∠ABD=90°，建立如图1的坐标系使得△ABC在yoz平面上，（2分）．

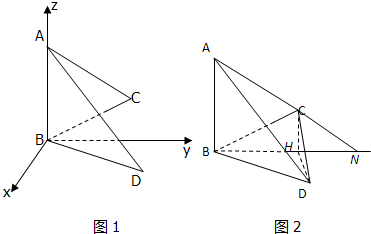
∵△ABD与△ABC成30°的二面角，∴∠DBY=30°，（3分）
又AB=BD=2，∴A（0，0，2），B（0，0，0），
C（0，

3

，1），D（1，

3

，0），（6分）
|CD|=

(1-0)2+( 3 - 3 )2+(0-1)2

=

2

，（7分）
解：（2）∵x轴与面ABC垂直，∴（1，0，0）是面ABC的一个法向量．
设CD与面ABC成的角为θ，
∵

CD

=（1，0，-1），（10分）
∴sinθ=

|(1，0，0)•(1，0，-1)|

12+02+02 12+02+(-1)2

=

2

2

．（12分）
∵θ∈[0，

π

2

]，∴θ=

π

4

；
∴CD与平面ABC的所成角是

π

4

．（14分）

点评：本题考查空间两点间的距离的求法，考查直线与平面所成角的大小的求法，解题时要恰当地建立空间直角坐标系，用向量法求解．