题目内容
5．
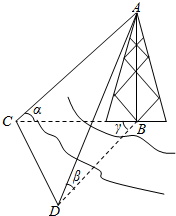河对岸有一个建筑物AB，建筑物的底部不可到达，利用量角器和米尺设计以下测量方案：选取与建筑物底部B在同一水平面内的两个测量点C和D．测得CD=a，在C点和D点测得塔顶A的仰角分别是α和β，且∠CBD=γ，试求出建筑物AB的高度．
分析 设AB=h，则BC=hcotα，BD=hcotβ，△BCD中，由余弦定理，可得方程，即可求塔高AB．
解答 解：设AB=h，则BC=hcotα，BD=hcotβ，
△BCD中，∠CBD=γ，CD=a，
由余弦定理，可得a2=h2cot2α+h2cot2β-2hcotα•hcotα•cosγ
∴h=$\sqrt{\frac{{a}^{2}}{co{t}^{2}α+co{t}^{2}β-2cotα•cotα•cosγ}}$．
点评 本题考查利用数学知识解决实际问题，考查余弦定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目