题目内容
17.已知数列{$\frac{{a}_{n}}{n+2}$}为等比数列,且a2=16,a3=40,则数列{$\frac{{4}^{n}}{{a}_{n}{a}_{n+1}}$}的前60项和为$\frac{10}{63}$.分析 设等比数列{$\frac{{a}_{n}}{n+2}$}的公比为q,由于a2=16,a3=40,可得$\frac{40}{3+2}$=$\frac{16}{2+2}×q$,解得q.可得an,再利用“裂项求和”即可得出.
解答 解:设等比数列{$\frac{{a}_{n}}{n+2}$}的公比为q,
∵a2=16,a3=40,
∴$\frac{40}{3+2}$=$\frac{16}{2+2}×q$,解得q=2.
∴$\frac{{a}_{n}}{n+2}$=$\frac{{a}_{2}}{4}$×qn-2=4×2n-2=2n,
∴an=(n+2)•2n,
∴$\frac{{4}^{n}}{{a}_{n}{a}_{n+1}}$=$\frac{{4}^{n}}{(n+2)•{2}^{n}(n+3)•{2}^{n+1}}$=$\frac{1}{2}(\frac{1}{n+2}-\frac{1}{n+3})$.
数列{$\frac{{4}^{n}}{{a}_{n}{a}_{n+1}}$}的前60项和=$\frac{1}{2}[(\frac{1}{3}-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{5})$+…+$(\frac{1}{n+2}-\frac{1}{n+3})]$
=$\frac{1}{2}(\frac{1}{3}-\frac{1}{n+3})$
=$\frac{n}{6(n+3)}$.
故答案为:$\frac{10}{63}$.
点评 本题考查了等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
8.方程y一1=$\sqrt{1-{x}^{2}}$表示的曲线是( )
| A. | 直线 | B. | 射线 | C. | 圆 | D. | 半圆 |
12.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过点F2且斜率为$\frac{2b}{a}$的直线l交直线2bx+ay=0于M,若M在以线段F1F2为直径的圆上,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.已知某几何体的三视图如图所示,则该几何体的体积是( )
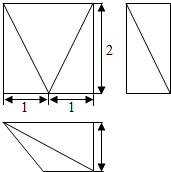

| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
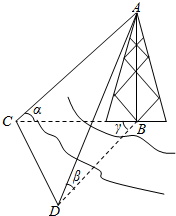 河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.
河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.