题目内容
20.已知函数f(x)=$\frac{{3}^{x}-{3}^{-x}}{2}$,求它的反函数f-1(x).分析 令y=$\frac{{3}^{x}-{3}^{-x}}{2}$,将式子变形用y表示出x,然后互换变量符号得出.
解答 解:令y=$\frac{{3}^{x}-{3}^{-x}}{2}$,则3x-3-x-2y=0,∴(3x)2-2y3x-1=0,
∴3x=$\frac{2y+\sqrt{4{y}^{2}+4}}{2}$=y+$\sqrt{{y}^{2}+1}$,∴x=log3(y+$\sqrt{{y}^{2}+1}$).
∴f-1(x)=log3(x+$\sqrt{{x}^{2}+1}$).
点评 本题考查了反函数的定义,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.方程y一1=$\sqrt{1-{x}^{2}}$表示的曲线是( )
| A. | 直线 | B. | 射线 | C. | 圆 | D. | 半圆 |
15.甲与其四位同事各有一辆私家车,车牌尾数分别是0、0、2、1、5,为遵守当地某月5日至9日5天的限行规定(奇数日车牌尾数为奇数的车通行,偶数日车牌尾数为偶数的车通行),五人商议拼车出行,每天任选一辆符合规定的车,但甲的车最多只能用-天,则不同的用车方案种数为( )
| A. | 5 | B. | 24 | C. | 32 | D. | 64 |
12.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1(-c,0)、F2(c,0),过点F2且斜率为$\frac{2b}{a}$的直线l交直线2bx+ay=0于M,若M在以线段F1F2为直径的圆上,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
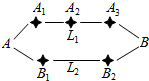 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.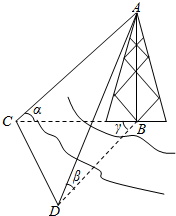 河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.
河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.