题目内容
15.设函数f(x)=x-$\frac{1}{x}$-a1nx.(1)当a=1时.求曲线y=f(x)在点(1,f(1))处的切线方程:
(2)若函数f(x)在定义域上为增函数,求实数a的取值范围:
(3)在(2)的条件下,若函数h(x)=x-lnx-$\frac{1}{e}$,?x1,x2∈[1,e]使得f(x1)≥h(x2)成立,求实数a的取值范围.
分析 (1)求出f(x)的导数,求得切线的斜率和切点,由点斜式方程即可得到所求切线的方程;
(2)由题意可得f′(x)≥0在(0,+∞)恒成立,即为1+$\frac{1}{{x}^{2}}$-$\frac{a}{x}$≥0,即有a≤x+$\frac{1}{x}$(x>0)的最小值,求出最小值,即可得到所求范围;
(3)运用导数求出f(x),h(x)的单调性,由题意可得可得f(x)max≥h(x)min,解不等式即可得到所求范围.
解答 解:(1)f(x)=x-$\frac{1}{x}$-1nx的导数为f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{1}{x}$,
曲线y=f(x)在点(1,f(1))处的切线斜率为k=1+1-1=1,
切点为(1,0),
则曲线y=f(x)在点(1,f(1))处的切线方程为y=x-1;
(2)由题意可得f′(x)≥0在(0,+∞)恒成立,
即为1+$\frac{1}{{x}^{2}}$-$\frac{a}{x}$≥0,即有a≤x+$\frac{1}{x}$(x>0)的最小值,
由x+$\frac{1}{x}$≥2,当且仅当x=1时,取得等号.
即有a≤2;
(3)由(2)可得a≤2时,f(x)在[1,e]递增;
函数h(x)=x-lnx-$\frac{1}{e}$的导数为h′(x)=1-$\frac{1}{x}$,
即有h′(x)≥0在[1,e]成立,即有h(x)在[1,e]递增,
由题意?x1,x2∈[1,e]使得f(x1)≥h(x2)成立,
可得f(x)max≥h(x)min,
即为f(e)≥h(1),即有e-$\frac{1}{e}$-a≥1-$\frac{1}{e}$,
解得a≤e-1.
点评 本题考查导数的运用:求切线的方程和单调区间,考查不等式恒成立问题的解法,以及存在性问题的解法,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | 2 | B. | 4 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
| A. | y2=8$\sqrt{2}$x | B. | y2=±4$\sqrt{2}$x | C. | y2=±4x | D. | y2=±8$\sqrt{2}$x |
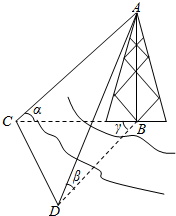 河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.
河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.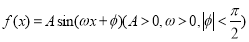 的部分图象如图所示.
的部分图象如图所示.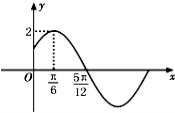
 ,
,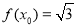 ,若g(x)=1+2cos2x,求g(x0)的值;
,若g(x)=1+2cos2x,求g(x0)的值; 上有解,求实数a的取值范围.
上有解,求实数a的取值范围.