题目内容
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点A(2,1),且直线l:x-2y-$\sqrt{6}$=0过椭圆C的一个焦点.(1)求椭圆C的方程;
(2)已知直线l′平行于直线l,且与椭圆C交于不同的两点M,N,记直线AM的倾斜角为θ1,直线AN的倾斜角为θ2,试探究θ1+θ2是否为定值,并说明理由.
分析 (1)由题意知c=$\sqrt{6}$,$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,求出a,b,由此能求出椭圆方程.
(2)θ1+θ2=π.理由如下:设直线l′的方程为x-2y+m=0,与$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1联立,可得8y2-4my+m2-8=0,利用韦达定理,由此得到kAM=-kAN,即可得出结论.
解答 解:(1)由题意,c=$\sqrt{6}$,$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,∴a=2$\sqrt{2}$,b=$\sqrt{2}$,
∴椭圆C的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1;
(2)直线l′的方程为x-2y+m=0,与$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1联立,可得8y2-4my+m2-8=0,
设M(x1,y1),N(x2,y2),
∴y1+y2=$\frac{m}{2}$,y1y2=$\frac{{m}^{2}}{8}$-1,
∴x1+x2=-m,x1x2=$\frac{{m}^{2}}{2}$-4,
∴kAM+kAN=$\frac{{y}_{1}-1}{{x}_{1}-2}$+$\frac{{y}_{2}-1}{{x}_{2}-2}$=$\frac{4{y}_{1}{y}_{2}-(2+m){(y}_{1}+{y}_{2})-({x}_{1}+{x}_{2})+4}{({x}_{1}-2)({x}_{2}-2)}$=0,
∴tanθ1+tanθ2=0,
∴θ1+θ2=π
点评 本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆方程的求法.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答.

| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
| A. | -$\frac{16}{65}$ | B. | $\frac{16}{65}$ | C. | $\frac{63}{65}$ | D. | -$\frac{63}{65}$ |
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
 在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.
在一次全国高中五省大联考中,有90万的学生参加,考后对所有学生成绩统计发现,英语成绩服从正态分布N(μ,σ2),如表用茎叶图列举了20名学生英语的成绩,巧合的是这20个数据的平均数和方差恰比所有90万个数据的平均数和方差都多0.9,且这20个数据的方差为49.9.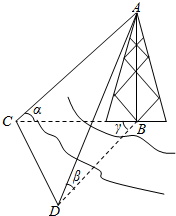 河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.
河对岸有一个建筑物AB,建筑物的底部不可到达,利用量角器和米尺设计以下测量方案:选取与建筑物底部B在同一水平面内的两个测量点C和D.测得CD=a,在C点和D点测得塔顶A的仰角分别是α和β,且∠CBD=γ,试求出建筑物AB的高度.