题目内容
(Ⅰ)已知x>0,y>0,且x+y=1,求
+
的最小值;
(Ⅱ)设0<x<2,求函数y=3
的最大值.
| 1 |
| x |
| 4 |
| y |
(Ⅱ)设0<x<2,求函数y=3
| x(2-x) |
考点:基本不等式
专题:不等式的解法及应用
分析:(Ⅰ)把
+
转化为(x+y)(
+
),展开后利用基本不等式求得最值.
(Ⅱ)根据x的范围判断出2-x>0,进而根据基本不等式的性质求得y的最大值.
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
(Ⅱ)根据x的范围判断出2-x>0,进而根据基本不等式的性质求得y的最大值.
解答:
(Ⅰ)已知x>0,y>0,且x+y=1,
则
+
=(x+y)(
+
)=
+
+5≥9,
当且仅当y=2x,即x=
,y=
时,
+
取得最小值9.
(Ⅱ)0<x<2,则2-x>0,
函数y=3
≤3•
=3,
当且仅当x=1时,y取得最大值3.
则
| 1 |
| x |
| 4 |
| y |
| 1 |
| x |
| 4 |
| y |
| y |
| x |
| 4x |
| y |
当且仅当y=2x,即x=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| x |
| 4 |
| y |
(Ⅱ)0<x<2,则2-x>0,
函数y=3
| x(2-x) |
| x+2-x |
| 2 |
当且仅当x=1时,y取得最大值3.
点评:本题主要考查了基本不等式的应用.基本不等式是解决最值问题时常用的方法,但要特别注意等号条件的满足.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且AD=AB=AA1=2,∠BAD=60°,E为AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且AD=AB=AA1=2,∠BAD=60°,E为AB的中点.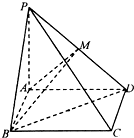 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.