题目内容
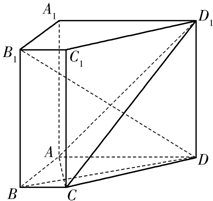
如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，且AD=AB=AA1=2，∠BAD=60°，E为AB的中点．（1）证明：AC1∥平面EB1C；
（2）求三棱锥C1-EB1C的体积．
考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：综合题,空间位置关系与距离
分析：（1）利用三角形的中位线及线面平行的判定定理即可证明；
（2）利用等体积转换，即可三棱锥C1-EB1C的体积
（2）利用等体积转换，即可三棱锥C1-EB1C的体积
解答：
（1）证明：连接BC1，B1C∩BC1=O，连接EO．
∵AE=EB，OB=OC1，∴EO∥AC1
∵AC1?面EB1C，EO?面EB1C
∴AC1∥面EB1C．
（2）解：∵AD=AB=AA1=2，∠BAD=60°，E为AB的中点．
∴VC1-EB1C=VE-C1B1C=
×
×2×2×
=
．
∵AE=EB，OB=OC1，∴EO∥AC1
∵AC1?面EB1C，EO?面EB1C
∴AC1∥面EB1C．
（2）解：∵AD=AB=AA1=2，∠BAD=60°，E为AB的中点．
∴VC1-EB1C=VE-C1B1C=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
点评：熟练掌握线面平行的判定定理、等体积转换是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
等差数列{an}满足a7+a8+a3=15，函数fn（x）=sin（
x+
），那么f5（a6）的值为（ ）
| π |
| n |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
如图，在直棱柱ABCD-A1B1C1D1中，AD∥BC，∠BAD=90°，AC⊥BD，BC=1，AD=AA1=3．
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜