题目内容
已知函数y=2sin（2x+
），
（1）求y的最大值及取得最大值时x的集合．
（2）用五点法作出它在长度为一个周期的闭区间上的简图；
（3）说明y=2sin（2x+
）的图象可由y=sinx的图象经过怎样的变换而得到．
| π |
| 3 |
（1）求y的最大值及取得最大值时x的集合．
（2）用五点法作出它在长度为一个周期的闭区间上的简图；
（3）说明y=2sin（2x+
| π |
| 3 |
考点：函数y=Asin（ωx+φ）的图象变换,五点法作函数y=Asin（ωx+φ）的图象
专题：三角函数的图像与性质
分析：（1）由条件利用正弦函数的定义域和值域求得y的最大值及取得最大值时x的集合．
（2）用五点法作函数y=Asin（ωx+φ）在一个周期上的简图．
（3）根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
（2）用五点法作函数y=Asin（ωx+φ）在一个周期上的简图．
（3）根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答：
解：（1）对于函数y=2sin（2x+
），当2x+
=2kπ+
，k∈z时，函数取得最大值为2，
此时，x的集合为{x|x=kπ+
，k∈z}．
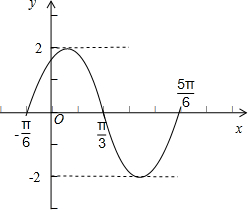
（2）列表：
作图：
（3）把y=sinx的图象向左平移
个单位，可得函数y=sin（x+
）的图象；
再把所得图象上点的横坐标变为原来的
倍，可得函数y=sin（2x+
）的图象；
再把所得图象上的点的纵坐标变为原来的2倍，可得函数y=2sin（2x+
）的图象．
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
此时，x的集合为{x|x=kπ+
| π |
| 12 |
（2）列表：
2x+
| 0 |
| π |
| 2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |
（3）把y=sinx的图象向左平移
| π |
| 3 |
| π |
| 3 |
再把所得图象上点的横坐标变为原来的
| 1 |
| 2 |
| π |
| 3 |
再把所得图象上的点的纵坐标变为原来的2倍，可得函数y=2sin（2x+
| π |
| 3 |
点评：本题主要考查正弦函数的定义域和值域，用五点法作函数y=Asin（ωx+φ）在一个周期上的简图，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设全集U={1，2，3，4}，集合S={l，3}，T={4}，则（∁US）∪T等于（ ）
| A、{2，4} | B、{4} |
| C、∅ | D、{1，3，4} |
等差数列{an}满足a7+a8+a3=15，函数fn（x）=sin（
x+
），那么f5（a6）的值为（ ）
| π |
| n |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
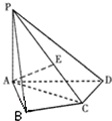如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．