题目内容
已知数列{an}中,a1=1,an+1=an+2n+1,且n∈N*.
(1)求数列{an}的通项公式;
(2)令bn=
,数列{bn}的前n项和为Tn.如果对于任意的n∈N*,都有Tn>m,求实数m的取值范围.
(1)求数列{an}的通项公式;
(2)令bn=
| 2n+1 |
| anan+1 |
考点:数列与不等式的综合,数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)由已知递推公式可利用叠加法求解数列的通项公式;
(2)求出数列{bn}的前n项和为Tn,求出数列的最值即可求出实数m的取值范围.
(2)求出数列{bn}的前n项和为Tn,求出数列的最值即可求出实数m的取值范围.
解答:
解:(1)∵an+1=an+2n+1,
∴an+1-an=2n+1
∴a2-a1=2+1
a3-a2=4+1
…
an-an-1=2(n-1)+1
以上n-1个式子相加可得,an-a1=2+4+…+2n-2+(n-1)=n2-1
∵a1=1,
∴an=n2;
(2)由(1)知bn=
=
-
,
∴Tn=(
-
)+(
-
)+…+(
-
)=1-
∴数列{bn}是递增数列,
∴最小值为1-
=
,只需要
>m,
∴实数m的取值范围(-∞,
).
∴an+1-an=2n+1
∴a2-a1=2+1
a3-a2=4+1
…
an-an-1=2(n-1)+1
以上n-1个式子相加可得,an-a1=2+4+…+2n-2+(n-1)=n2-1
∵a1=1,
∴an=n2;
(2)由(1)知bn=
| 2n+1 |
| anan+1 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
∴Tn=(
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
∴数列{bn}是递增数列,
∴最小值为1-
| 1 |
| (1+1)2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴实数m的取值范围(-∞,
| 3 |
| 4 |
点评:本题考查了利用递推公式求数列的通项公式以及数列求和的应用,考查了累加法.属于基本方法的简单应用

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
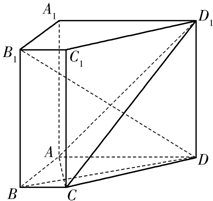 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.