题目内容
已知函数f(x)=
cosωx,g(x)=sin(ωx-
)ω>0),且g(x)的最小正周期为π.
(Ⅰ)若f(a)=
,a∈[-π,π],求a的值;
(Ⅱ)求函数y=f(x)+g(x)的单调增区间.
| 3 |
| π |
| 3 |
(Ⅰ)若f(a)=
| ||
| 2 |
(Ⅱ)求函数y=f(x)+g(x)的单调增区间.
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)根据g(x)的最小正周期为π,可以求得ω的值,从而得到f(x)的解析式,利用f(a)=
可以求得α的取值;
(Ⅱ)将函数y=f(x)+g(x)运用两角和差公式进行化简变形,从而得到 y=sin(2x+
),将2x+
看作一个整体,运用正弦函数的单调性,即可求得答案.
| ||
| 2 |
(Ⅱ)将函数y=f(x)+g(x)运用两角和差公式进行化简变形,从而得到 y=sin(2x+
| π |
| 3 |
| π |
| 3 |
解答:
解:(Ⅰ)解:因为g(x)=sin(ωx-
)的最小正周期π,
∴
=π,解得ω=2,
由f(α)=
,得
cos2α=
,
即cos2α=
,
∴2α=2kπ±
,k∈Z,
∵α∈[-π,π],
∴α∈{-
,-
,
,
};
(Ⅱ)函数 y=f(x)+g(x)=
cos2x+sin(2x-
)
=
cos2x+sin2xcos
-cos2xsin
=
sin2x+
cos2x
=sin(2x+
),
由2kπ-
≤2x+
≤2kπ+
,
解得kπ-
≤x≤kπ+
,
所以函数y=f(x)+g(x)的单调增区间为[kπ-
,kπ+
],k∈Z.
| π |
| 3 |
∴
| 2π |
| |ω| |
由f(α)=
| ||
| 2 |
| 3 |
| ||
| 2 |
即cos2α=
| ||
| 2 |
∴2α=2kπ±
| π |
| 4 |
∵α∈[-π,π],
∴α∈{-
| 7π |
| 8 |
| π |
| 8 |
| π |
| 8 |
| 7π |
| 8 |
(Ⅱ)函数 y=f(x)+g(x)=
| 3 |
| π |
| 3 |
=
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得kπ-
| 5π |
| 12 |
| π |
| 12 |
所以函数y=f(x)+g(x)的单调增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
点评:本题考查了三角恒等变换,主要考查了三角函数的两角和差公式,考查了三角函数求值问题,若是求角,则必须先确定的角的范围再决定角的值.形如y=Asin(ωx+φ)形式的性质问题,一般都是用整体代换的思想,转化为三角函数的性质进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
定义在(1,+∞)上的函数f(x)满足两个条件:(1)对任意的x∈(1,+∞)恒有f(2x)=2f(x)成立;(2)当x∈(1,2)时,f(x)=2-x;记函数g(x)=f(x)-k(x-1),若函数g(x)恰有两个零点,则实数k的取值范围是( )
| A、(1,2) | ||
B、(1,
| ||
C、(
| ||
D、(
|
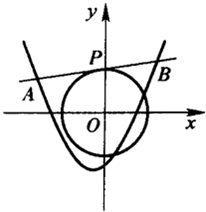 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;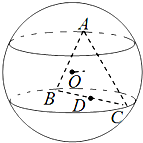 正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为
正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为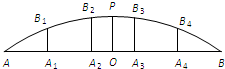 圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.
圆拱桥的一孔圆拱如图所示,该圆拱是一段圆弧,其跨度AB=20米,拱高OP=4米,在建造时每隔4米需用一根支柱支撑.