题目内容
5.在△ABC中,a,b,c分别是角A,B,C的对边,其外接圆半径为1,(c-2a)cosB+bcosC=0.(1)求角B的大小;
(2)求△ABC周长的取值范围.
分析 (1)根据题意,由正弦定理可以将(c-2a)cosB+bcosC=0整理变形可得2sinA•cosB=sinC•cosB+sinBcosC,又由三角函数的和差公式可得2sinA•cosB=sin(B+C),进而可得2sinA•cosB=sinA,即cosB=$\frac{1}{2}$,由B的范围可得B的值.
(2)根据题意,由正弦定理可得b的值,同时可得a+c=2(sinA+sinC),由三角函数的和差公式变形可得a+c=2$\sqrt{3}$sin(C+$\frac{π}{6}$),结合C的范围,计算可得a+c的范围,由b的值,即可得答案.
解答 解:(1)根据题意,(2a-c)cosB=bcosC,
由正弦定理得:(2sinA-sinC)cosB=sinBcosC,即2sinA•cosB-sinC•cosB=sinBcosC
变形可得:2sinA•cosB=sinC•cosB+sinBcosC
∴2sinA•cosB=sin(B+C)
∵在△ABC中,sin(B+C)=sinA
∴2sinA•cosB=sinA,即cosB=$\frac{1}{2}$,
则B=$\frac{π}{3}$;
(2)根据题意,由(1)可得B=$\frac{π}{3}$,sinB=$\frac{\sqrt{3}}{2}$,又由正弦定理b=2RsinB=$\sqrt{3}$,
a=2RsinA=2sinA,c=2RsinC=2sinC;
则a+c=2(sinA+sinC)=2[sin($\frac{2π}{3}$-C)+sinC]=2[$\frac{\sqrt{3}}{2}$cosC+$\frac{3}{2}$sinC]=2$\sqrt{3}$sin(C+$\frac{π}{6}$),
又由0<C<$\frac{2π}{3}$,则$\frac{π}{6}$<C+$\frac{π}{6}$<$\frac{5π}{6}$,
则有$\frac{1}{2}$<sin(C+$\frac{π}{6}$)≤1,
故$\sqrt{3}$<a+c≤2$\sqrt{3}$,
则有2$\sqrt{3}$<a+b+c≤3$\sqrt{3}$,
即△ABC周长的取值范围为(2$\sqrt{3}$,3$\sqrt{3}$].
点评 本题考查正弦定理的应用,涉及两角和差的正弦公式、三角函数的单调性,关键是正确运用三角函数的和差公式,对三角函数恒等变形.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,1) |
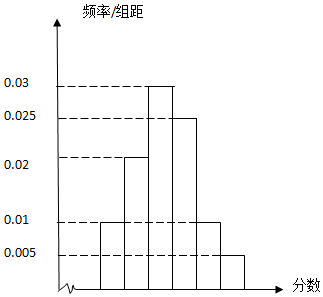 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示(I)用每组区间的中点值代表该组的数据,估算这批考生的平均成绩;
(II)现从及格的学生中,用分层抽样的方法抽取了70名学生(其中女生有34名),已知成绩“优异”(超过90分)的女生有1名,能否有95%的把握认为数学成绩优异与性别有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
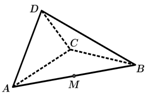 如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.
如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.