��Ŀ����
13����ֱ������ϵxoy��ԲC�IJ�������Ϊ$\left\{\begin{array}{l}x=2+3cos��\\ t=3sin��\end{array}\right.$����Ϊ����������ԭ��OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ$��=\frac{��}{4}��{�ѡ�R}��$����1����ԲC��ֱ�����귽�̼���Բ��C��ֱ�����ꣻ
��2����ֱ��l������C����A��B���㣬���ABC�������
���� ��1���������Ǻ����Ļ�����ϵʽ��ת��Բ�IJ�������Ϊ��ͨ���̣�Ȼ�����Բ��Բ�����ꣻ
��2�����ֱ�߷��̣�����Բ�ĵ�ֱ�ߵľ��롢�뾶�����ҳ������㹴�ɶ��������д����Ȼ����������ε������
��� �⣺����ԲC��$\left\{{\begin{array}{l}{x=2+3cos��}\\{y=3sin��}\end{array}}\right.$����Ϊ��������ԲC��ֱ�����귽�̣���x-2��2+y2=9��
Բ��C��ֱ������C��2��0��������4�֣�
����1�㣮ֱ��l�ļ����귽��Ϊ$��=\frac{��}{4}��{�ѡ�R}��$��
�ɵã�ֱ��l��ֱ�����귽�̣�x-y=0������5�֣�
2�㣮Բ��C��2��0����ֱ��l�ľ���$d=\frac{|2-0|}{{\sqrt{2}}}=\sqrt{2}$��ԲC�İ뾶r=3��
�ҳ�$|AB|=2\sqrt{{r^2}-{d^2}}=2\sqrt{7}$������8�֣�
3�㣮��ABC�����=$\frac{1}{2}|AB|��d=\frac{1}{2}��2\sqrt{7}��\sqrt{2}=\sqrt{14}$������10�֣�
���� ���⿼�鼫����ϵ�������������ͨ���̵Ļ���������ת��˼���Լ�����������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
18����a��b��0��a+b=1����x=��$\frac{1}{a}$��b��y=log${\;}_{��\frac{1}{a}+\frac{1}{b}��}$ab��z=log${\;}_{\frac{1}{b}}$a����x��y��z�Ĵ�С��ϵ�ǣ�������
| A�� | y��x��z | B�� | y��z��x | C�� | x��y��z | D�� | z��y��x |
2������y=kx+2�뺯��$y=\frac{1}{|x|}$��ͼ�����������������㣬����k����ʽ��k-2��a-k��0�н⣬��ʵ��a��ȡֵ��Χ�ǣ�������
| A�� | $-1��a��\frac{1}{3}$ | B�� | $a��\frac{1}{3}$ | C�� | a��-1 | D�� | a��1 |
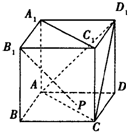 ��ͼ��������ABCD-A1B1C1D1���ⳤΪ1����P���ı���ABCD�ڼ���߽����˶����ҵ�P����B1�ľ���Ϊ$\sqrt{2}$��
��ͼ��������ABCD-A1B1C1D1���ⳤΪ1����P���ı���ABCD�ڼ���߽����˶����ҵ�P����B1�ľ���Ϊ$\sqrt{2}$��