题目内容
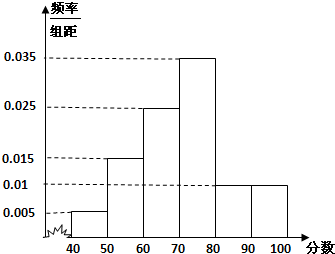
为统计某校学生数学学业水平测试成绩,现抽出40名学生成绩,得到样本频率分布直方图,如图所示,规定不低于60分为及格,不低于85分为优秀.
(1)估计总体的及格率;
(2)求样本中优秀人数;
(3)若从样本中优秀的学生里抽出2人,求这两人至少有一人数学成绩不低于90分的概率.

(1)估计总体的及格率;
(2)求样本中优秀人数;
(3)若从样本中优秀的学生里抽出2人,求这两人至少有一人数学成绩不低于90分的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(1)由题意分析直方图,结合频率=矩形的高×组距,累加不低于60分段的频率,进而可得答案.
(2)由题意分析直方图,结合频率=矩形的高×组距,累加不低于85分段的频率,进而根据频数=频率×样本容量,得到优秀人数;
(3)分别求出从样本中优秀的学生里抽出2人的基本事件总数和这两人至少有一人数学成绩不低于90分的基本事件个数,代入古典概型的概率计算公式,可得答案.
(2)由题意分析直方图,结合频率=矩形的高×组距,累加不低于85分段的频率,进而根据频数=频率×样本容量,得到优秀人数;
(3)分别求出从样本中优秀的学生里抽出2人的基本事件总数和这两人至少有一人数学成绩不低于90分的基本事件个数,代入古典概型的概率计算公式,可得答案.
解答:
解:(1)由题意分析直方图,
可得不低于60分段的频率为:10×[1-(0.005+0.015)]=0.8,
故及格率为80%------------(2分)
(2)由题意分析直方图,
可得不低于85分段的频率为:10×(
×0.01+0.01)=0.15,
故优秀率为15%,
故优秀人数40×15%=6人--------------(4分)
(3)由(2)可得样本中优秀的学生中,85分-90分有2人,设为b1、b2;
90分-100分有4人,设为c1、c2、c3、c4,------------(6分)
那么一次试验的全部结果为:
b1b2,b1c1,b1c2,b1c3,b1c4,b2c1,
b2c2,b2c3,b2c4,b2c1,c1c3,c1c4,
c2c3,c2c4,c3c4共15个结果,--------------------(8分)
其中这两人至少有一人数学成绩不低于90分的结果有:
b1c1,b1c2,b1c3,b1c4,b2c1,
b2c2,b2c3,b2c4,b2c1,c1c3,c1c4,
c2c3,c2c4,c3c4共14个结果
故这两人至少有一人数学成绩不低于90分的概率p=
-----------(10分)
可得不低于60分段的频率为:10×[1-(0.005+0.015)]=0.8,
故及格率为80%------------(2分)
(2)由题意分析直方图,
可得不低于85分段的频率为:10×(
| 1 |
| 2 |
故优秀率为15%,
故优秀人数40×15%=6人--------------(4分)
(3)由(2)可得样本中优秀的学生中,85分-90分有2人,设为b1、b2;
90分-100分有4人,设为c1、c2、c3、c4,------------(6分)
那么一次试验的全部结果为:
b1b2,b1c1,b1c2,b1c3,b1c4,b2c1,
b2c2,b2c3,b2c4,b2c1,c1c3,c1c4,
c2c3,c2c4,c3c4共15个结果,--------------------(8分)
其中这两人至少有一人数学成绩不低于90分的结果有:
b1c1,b1c2,b1c3,b1c4,b2c1,
b2c2,b2c3,b2c4,b2c1,c1c3,c1c4,
c2c3,c2c4,c3c4共14个结果
故这两人至少有一人数学成绩不低于90分的概率p=
| 14 |
| 15 |
点评:本题考查古典概型的计算,涉及列举法的应用,注意结合题意中“写出所有可能的结果”的要求,使用列举法,注意按一定的顺序列举,做到不重不漏.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
在△ABC中,A,B,C成等差数列,则tan
+tan
+
tan
•tan
的值是( )
| A |
| 2 |
| C |
| 2 |
| 3 |
| A |
| 2 |
| C |
| 2 |
A、±
| ||||
B、-
| ||||
C、
| ||||
D、
|
等比数列{an}的各项均为正数,且a4a5+a3a6=18,则log3a1+log3a2+…+log3a8=( )
| A、12 | B、10 | C、8 | D、6 |
1+C271+C272+C2727除以3所得余数为( )
| A、0 | B、1 | C、2 | D、3 |
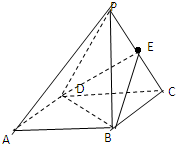 如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD为正方形,E是PC的中点,