题目内容
已知：函数f（x）=x3-ax（a∈R），且x=1是f（x）的一个极值点．
（1）求a的值；
（2）求过函数f（x）图象上点A（2，f（2））处的切线方程．
（1）求a的值；
（2）求过函数f（x）图象上点A（2，f（2））处的切线方程．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题：
分析：（1）根据函数导数和极值之间的关系即可求a的值；
（2）求函数的导数，根据导数的几何意义即可求出切线方程．
（2）求函数的导数，根据导数的几何意义即可求出切线方程．
解答：
解：（1）函数的导数f′（x）=2x2-a，
∵x=1是f（x）的一个极值点，∴f′（1）=2-a=0，
解得a=2．
（2）当a=2时，则f（x）=x3-2x，f′（x）=2x2-2，
则f（2）=8-4=4，f′（2）=8-2=6，
则在A处的切线方程为y-4=6（x-2），
即6x-y-8=0．
∵x=1是f（x）的一个极值点，∴f′（1）=2-a=0，
解得a=2．
（2）当a=2时，则f（x）=x3-2x，f′（x）=2x2-2，
则f（2）=8-4=4，f′（2）=8-2=6，
则在A处的切线方程为y-4=6（x-2），
即6x-y-8=0．
点评：本题主要考查函数的导数和极值之间的关系以及函数切线的求解，根据导数的几何意义是解决本题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目
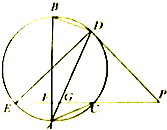如图所示，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG=PD，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F．（Ⅰ）求证：AB为圆的直径；
（Ⅱ）若AC=BD，AB=5，求弦DE的长．
已知f（x）=2012x+
+2014，α，β表示锐角三角形的两个内角，则下列结论正确的是（ ）
| 2013 |
| x |
| A、f（cosα）＞f（cosβ） |
| B、f（sinα）＞f（sinβ） |
| C、f（sinα）＞f（cosβ） |
| D、f（sinα）＜f（cosβ） |