题目内容
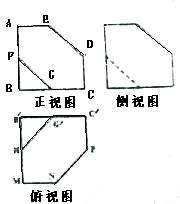 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )| A、5 | ||
B、7-6
| ||
C、8-6
| ||
| D、4 |
考点:棱柱、棱锥、棱台的体积
专题:计算题
分析:画出对应的立体图形,并将截去的多面体分成几个可求体积的多面体,所以所得多面体的体积应为正方体的体积减去截去的多面体的体积.
解答:
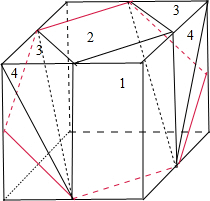 解:根据三视图画出立体图形,如下图:
解:根据三视图画出立体图形,如下图:
根据图形可看出,截得的多面体的面积应是V正方体-(V1+V2+2V3+2V4);
根据已知的边的长度,V1=
×1×1×2=1,V2=
×
×2×
=2,2V3=2×[
×(
×1×1)×2]=
,2V4=2×[
×(
×1×1)×1]=
;
V正方体=2×2×2=8;
∴V=V正方体-(V1+V2+2V3+2V4)=8-4=4.
故选:D.
 解:根据三视图画出立体图形,如下图:
解:根据三视图画出立体图形,如下图:根据图形可看出,截得的多面体的面积应是V正方体-(V1+V2+2V3+2V4);
根据已知的边的长度,V1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
V正方体=2×2×2=8;
∴V=V正方体-(V1+V2+2V3+2V4)=8-4=4.
故选:D.
点评:考查由三视图画出对应的立体图形的能力,以及将不规则的多面体分成几个可求出体积的几个多面体来求体积的方法.

练习册系列答案
相关题目
若函数f(x)=
x3+x2-
在区间(a,a+5)内存在最小值,则实数a的取值范围是( )
| 1 |
| 3 |
| 2 |
| 3 |
| A、[-5,0) |
| B、(-5,0) |
| C、[-3,0) |
| D、(-3,0) |
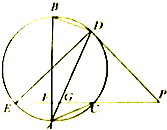 如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.