题目内容
一位同学设计计算13+23+…+103的程序框图时把图中的①②的顺序颠倒了，则输出的结果比原结果大 ．
考点：程序框图
专题：图表型,算法和程序框图
分析：执行程序框图，第一个处理框为s=s+i3，第二个处理框为i=i+1时，S1=13+23+…+103，若把图中的①②的顺序颠倒，执行程序可知，S2=23+…+103＜S1．
解答：
解：程序框图的功能是计算13+23+…+103，则第一个处理框应为s=s+i3，第二个处理框应为i=i+1，S1=13+23+…+103
若把图中的①②的顺序颠倒，执行程序可知，S2=23+…+103＜S1．
故输出的结果比原结果小，
故答案为：错误．
若把图中的①②的顺序颠倒，执行程序可知，S2=23+…+103＜S1．
故输出的结果比原结果小，
故答案为：错误．
点评：本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，属于基本知识的考查．
练习册系列答案
智能训练练测考系列答案
相关题目
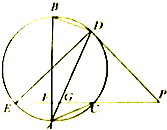如图所示，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG=PD，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F．（Ⅰ）求证：AB为圆的直径；
（Ⅱ）若AC=BD，AB=5，求弦DE的长．
已知f（x）=2012x+
+2014，α，β表示锐角三角形的两个内角，则下列结论正确的是（ ）
| 2013 |
| x |
| A、f（cosα）＞f（cosβ） |
| B、f（sinα）＞f（sinβ） |
| C、f（sinα）＞f（cosβ） |
| D、f（sinα）＜f（cosβ） |
已知集合A={a2，a+2}，B={3a-2，2a+1}，若A=B，则实数a的值为（ ）
| A、2 | B、1 | C、-1或1 | D、1或2 |
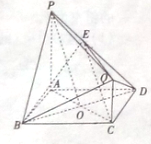如图，直线PA，QC都与正方形ABCD所在平面垂直，AB=PA=2QC=2，AC与BD相交于点O，E在线段PD上且CE∥平面PBQ
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD||BC，PD⊥底面ABCD，