题目内容
在△ABC内，a、b、c分别为角A、B、C所对的边，且满足sinA+sinB=2sinC，a=2b．
（1）求cosA的值；
（2）若S△ABC=
，求△ABC三边的长．
（1）求cosA的值；
（2）若S△ABC=
| 3 |
| 4 |
| 15 |
考点：正弦定理
专题：计算题,解三角形
分析：（1）利用正弦定理，再用余弦定理，即可求cosA的值；
（2）由S△ABC=
，结合三角形的面积公式求出b，即可求△ABC三边的长．
（2）由S△ABC=
| 3 |
| 4 |
| 15 |
解答：
解：（1）∵sinA+sinB=2sinC，
∴a+b=2c，
∵a=2b，
∴c=
b，
∴cosA=
=-
；
（2）由（1）知，sinA=
，
∵S△ABC=
，
∴
b×
b×
=
，
∴b=2，
∴a=4，c=3．
∴a+b=2c，
∵a=2b，
∴c=
| 3 |
| 2 |
∴cosA=
b2+
| ||
2b×
|
| 1 |
| 4 |
（2）由（1）知，sinA=
| ||
| 4 |
∵S△ABC=
| 3 |
| 4 |
| 15 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 4 |
| 3 |
| 4 |
| 15 |
∴b=2，
∴a=4，c=3．
点评：正弦定理与余弦定理是解决三角形问题的常用公式，必须记忆清楚．
练习册系列答案
相关题目
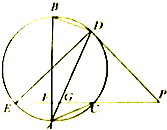如图所示，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG=PD，连接DG并延长交圆于点A，作弦AB垂直EP，垂足为F．
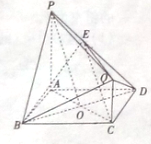如图，直线PA，QC都与正方形ABCD所在平面垂直，AB=PA=2QC=2，AC与BD相交于点O，E在线段PD上且CE∥平面PBQ