题目内容
3.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,-4),|$\overrightarrow{c}$|=$\sqrt{5}$,若($\overrightarrow{c}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=$\frac{15}{2}$,则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为( )| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
分析 求出$\overrightarrow{a}•\overrightarrow{c}$,再计算cos<$\overrightarrow{a},\overrightarrow{c}$>即可得出.
解答 解:∵($\overrightarrow{c}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=$\overrightarrow{a}•\overrightarrow{c}$-$\overrightarrow{a}•\overrightarrow{b}$=$\frac{15}{2}$,$\overrightarrow{a}•\overrightarrow{b}$=-2-8=-10,
∴$\overrightarrow{a}•\overrightarrow{c}$=$\frac{15}{2}$-10=-$\frac{5}{2}$,
∴cos<$\overrightarrow{a},\overrightarrow{c}$>=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}$=$\frac{-\frac{5}{2}}{\sqrt{5}×\sqrt{5}}$=-$\frac{1}{2}$,
∴$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为120°.
故选D.
点评 本题考查了平面向量的数量积运算,属于中档题.

练习册系列答案
相关题目
17.一段长为36m的篱笆围成一个矩形菜园,求这个矩形菜园的最大面积( )
| A. | 79 | B. | 80 | C. | 81 | D. | 82 |
18.$tan(-\frac{π}{4})$=( )
| A. | 1 | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
8.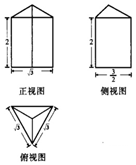 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
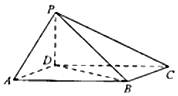 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.