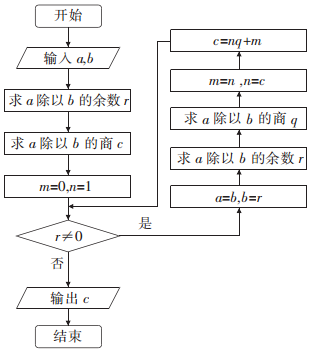
题目内容
18.已知函数f(x)=lnx,g(x)=$\frac{a}{x}$(a>0),设F(x)=f(x)+g(x).(1)求函数F(x)的单调区间;
(2)若以函数y=F(x)(x∈(0,3])图象上任意一点P(x0,y0)为切点的切线的斜率k≤$\frac{1}{2}$恒成立,求实数a的最小值.
分析 (1)求出F(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,注意定义域(0,+∞);
(2)求出导数,由导数的几何意义可得$\frac{{x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$(0<x0≤3)恒成立?a≥(-$\frac{1}{2}$x02+x0)max,运用二次函数的最值求法,即可得到最大值,进而得到a的最小值.
解答 解:(1)F(x)=lnx+$\frac{a}{x}$(x>0),F′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,a>0,
当x>a,F′(x)>0,f(x)在(a,+∞)单调递增,
当0<x<a,F′(x)<0,F(x)在(0,a)单调递减,
则F(x)的增区间为(a,+∞),减区间为(0,a);
(2)由y′=$\frac{x-a}{{x}^{2}}$,a>0(0<x≤3),
k=y′|${\;}_{x={x}_{0}}^{\;}$=$\frac{{x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$(0<x0≤3)恒成立?a≥(-$\frac{1}{2}$x02+x0)max,
当x0=1时,-$\frac{1}{2}$x02+x0 取得最大值$\frac{1}{2}$,
∴a≥$\frac{1}{2}$,
∴amin=$\frac{1}{2}$.
点评 本题考查利用导数研究函数的单调性,考查函数恒成立问题,考查化归思想的综合运用,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
13.$\overrightarrow{a}$,$\overrightarrow{b}$都为向量,则下列式子正确的是( )
| A. | $\overrightarrow{a}$•|$\overrightarrow{a}$|=$\overrightarrow{a}$2 | B. | ($\overrightarrow{a}$•$\overrightarrow{b}$)2=$\overrightarrow{a}$2•$\overrightarrow{b}$2 | C. | ($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}$•$\overrightarrow{c}$) | D. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| |
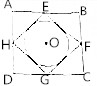 已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.
已知四边形ABCD中,E,F,G,H分别是线段AB,BC,CD,DA的中点,圆O为四边形EFGH的内切圆,则在正方形ABCD内投一点,该点落在圆O内的概率为$\frac{π}{8}$.