题目内容
已知sinα•cosα=
,且
<α<
,则cosα-sinα=( )
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用正弦函数与余弦函数的单调性可知当
<α<
,时,则cosα-sinα<0,于是可对所求关系式平方后再开方即可.
| π |
| 4 |
| π |
| 2 |
解答:
解:∵
<α<
,
∴cosα<sinα,即cosα-sinα<0,
设cosα-sinα=t(t<0),
则t2=1-2sinαcosα=1-
=
,
∴t=-
,即cosα-sinα=-
.
故选:D.
| π |
| 4 |
| π |
| 2 |
∴cosα<sinα,即cosα-sinα<0,
设cosα-sinα=t(t<0),
则t2=1-2sinαcosα=1-
| 1 |
| 4 |
| 3 |
| 4 |
∴t=-
| ||
| 2 |
| ||
| 2 |
故选:D.
点评:本题考查三角函数的化简求值,着重考查正弦函数与余弦函数的单调性,判断知cosα-sinα<0是关键,考查分析、运算能力,属于基本知识的考查.

练习册系列答案
相关题目
已知集合A={x|log4x<1},集合B={x|2x<8},则A∩B等于( )
| A、(-∞,4) |
| B、(0,4) |
| C、(0,3) |
| D、(-∞,3) |
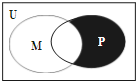 设全集U=Z,集合M={1,2}与P={x||x|<2,x∈Z}关系的韦恩(venn)图如图所示,则阴影部分所示的集合为( )
设全集U=Z,集合M={1,2}与P={x||x|<2,x∈Z}关系的韦恩(venn)图如图所示,则阴影部分所示的集合为( )| A、{-1,0} |
| B、{-2,-1,0} |
| C、{0,1,2} |
| D、{0,1} |
集合A={x|x2-2x>0},集合B是函数y=lg(2-x)的定义域,则A∩B=( )
| A、(-∞,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,+∞) |