题目内容
已知函数f（x）=|2x-2|，若m≠n，且f（m）=f（n），则m+n的取值范围是（ ）
| A、（1，+∞） |
| B、（2，+∞） |
| C、（-∞，1） |
| D、（-∞，2） |
考点：指数函数的图像变换
专题：函数的性质及应用,不等式的解法及应用
分析：由题意f（x）=|2x-2|，由f（m）=f（n），可得2-2m=2n-2，故2m+2n=4，
再利用基本不等式求解．
再利用基本不等式求解．
解答：
解：不妨设m＜n，
由f（m）=f（n），可得2-2m=2n-2，
∴2m+2n=4，
∴4=2m+2n=≥2
，
当且仅当2m=2n时，即m=n时取等号，而m≠n，故上述等号不成立，
∴2m+n＜4，
∴m+n＜2
∴m+n的取值范围是（-∞，2）
故选：D．
由f（m）=f（n），可得2-2m=2n-2，
∴2m+2n=4，
∴4=2m+2n=≥2
| 2m+n |
当且仅当2m=2n时，即m=n时取等号，而m≠n，故上述等号不成立，
∴2m+n＜4，
∴m+n＜2
∴m+n的取值范围是（-∞，2）
故选：D．
点评：此题考查了利用绝对值的性质脱去绝对值，同时考查基本不等式的应用，注意，利用基本不等式要验证等号成立的条件．
练习册系列答案
相关题目
已知集合A={x|log4x＜1}，集合B={x|2x＜8}，则A∩B等于（ ）
| A、（-∞，4） |
| B、（0，4） |
| C、（0，3） |
| D、（-∞，3） |
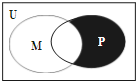设全集U=Z，集合M={1，2}与P={x||x|＜2，x∈Z}关系的韦恩（venn）图如图所示，则阴影部分所示的集合为（ ）| A、{-1，0} |
| B、{-2，-1，0} |
| C、{0，1，2} |
| D、{0，1} |