题目内容
18.在△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bsinb,且$B>\frac{π}{2}$,则sinA+sinC的最大值是$\frac{9}{8}$.分析 利用正弦定理化简得出A,B的关系,用A表示出C,利用三角函数恒等变换化简得出sinA+sinC关于sinA的函数,求出此函数的最大值即可.
解答 解:∵acosA=bsinA,∴$\frac{a}{sinA}=\frac{b}{cosA}$,
又由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,
∴sinB=cosA=sin($\frac{π}{2}$-A),
∵B>$\frac{π}{2}$,
∴π-B=$\frac{π}{2}$-A.
∴B=A+$\frac{π}{2}$.
∴C=π-A-B=$\frac{π}{2}$-2A.
∴sinA+sinC=sinA+cos2A=-2sin2A+sinA+1=-2(sinA-$\frac{1}{4}$)2+$\frac{9}{8}$.
∵0<A<$\frac{π}{2}$,0<$\frac{π}{2}$-2A<$\frac{π}{2}$,
∴0<A<$\frac{π}{4}$,
∴0<sinA<$\frac{\sqrt{2}}{2}$.
∴当sinA=$\frac{1}{4}$时,sinA+sinC取得最大值$\frac{9}{8}$.
故答案为:$\frac{9}{8}$.
点评 本题考查了三角函数的恒等变换,正弦定理,二次函数的最值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.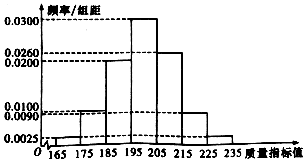 某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
 某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:| 质量指标值m | m<185 | 185≤m<205 | M≥205 |
| 等级 | 三等品 | 二等品 | 一等品 |
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
9.已知数列{an}满足递推关系:an+1=$\frac{{a}_{n}}{{a}_{n}+1}$,a1=$\frac{1}{2}$,则a2017=( )
| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{2018}$ | D. | $\frac{1}{2019}$ |
6.在△ABC中,a,b,c分别为角A,B,C所对的边,若(a+c+b)(b+a-c)=3ab,则C=( )
| A. | 150° | B. | 60° | C. | 120° | D. | 30° |
3.计算2sin275°-1的值等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.高二(7)班参加冬令营的6位同学排成一排照相,甲乙必须相邻且甲、乙、丙必须从左到右的排法种数为( )
| A. | 120 | B. | 60 | C. | 36 | D. | 72 |
7.在公比为2的等比数列{an}中,a1a3=6a2,则a4等于( )
| A. | 4 | B. | 8 | C. | 12 | D. | 24 |