题目内容
20.已知集合A={x|$\frac{2x-1}{x-2}>1$},B={x|-3<x<4,x∈Z},则A∩B=( )| A. | {-2,-1,0,1,2,3} | B. | {-2,-1,0,1,3} | C. | {-2,3} | D. | {3} |
分析 利用交集定义求解.
解答 解:由$\frac{2x-1}{x-2}>1$,得到$\frac{x+1}{x-2}$>0,即(x+1)(x-2)>0,解得x<-1,或x>2,
∴A=(-∞,-1)∪(2,+∞),
∵B={x|-3<x<4,x∈Z}={-2,-1,0,1,2,3},
∴A∩B={-2,3}.
故选:C.
点评 本题考查交集的求法,是基础题,解题时要认真审题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
11.当x→0时,下列4个无穷小量中比其它3个更高阶的无穷小量是( )
| A. | 1n(1+x) | B. | ex-1 | C. | tanx-sinx | D. | 1-cosx |
5.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
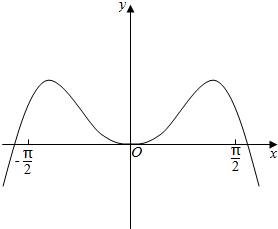

| A. | x2cosx | B. | sinx2 | C. | xsinx | D. | x2-$\frac{1}{6}$x4 |