题目内容
9.下列函数中,既是奇函数又是增函数的是( )| A. | y=3x | B. | y=x2 | C. | y=lnx | D. | y=x|x| |
分析 利用函数的奇偶性的定义、单调性的定义,即可得出结论.
解答 解:对于A,B,C,不是奇函数;
对于D是,f(-x)=-x|-x|=-f(x)是奇函数,f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,是增函数,
故选D.
点评 本题考查函数的奇偶性的定义、单调性的定义,比较基础.

练习册系列答案
相关题目
20.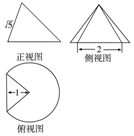 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )| A. | $π+\frac{2}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{3}{4}π+\frac{2}{3}$ | D. | $\frac{3}{4}π+\frac{1}{3}$ |
17.定义在R上的函数y=f(x)满足:f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)-ex>2016(其中e为自然对数的底数)的解集为( )
| A. | (2016,+∞) | B. | (-∞,0)∪(2016,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (0,+∞) |
18.已知点(x,y)满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$,则$z=\frac{y}{x+1}$的最小值为( )
| A. | 3 | B. | $\frac{7}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
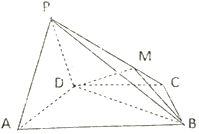 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.