题目内容
14.若函数y=sin(πx+φ)过点$({\frac{1}{6},1})$,则f(0)=$\frac{\sqrt{3}}{2}$.分析 将坐标代入求解φ,可得函数y=sin(πx+φ)的解析式,再求解f(0)即可.
解答 解:∵函数y=sin(πx+φ)过点$({\frac{1}{6},1})$,
∴1=sin($\frac{π}{6}+$φ)
得:φ$+\frac{π}{6}$=$\frac{π}{2}+2kπ$,(k∈Z)
φ=$\frac{π}{3}+2kπ$.
那么:函数y=sin($πx+\frac{π}{3}+2kπ$),
当x=0时,可得y=sin($\frac{π}{3}+2kπ$)=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$.
故f(0)=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征和计算化简能力,属于中档题

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.已知集合M={x|-1≤x<3,x∈R},N={-1,0,1,2,3},则M∩N=( )
| A. | {-1,0,2,3} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
9.下列函数中,既是奇函数又是增函数的是( )
| A. | y=3x | B. | y=x2 | C. | y=lnx | D. | y=x|x| |
19.在一个封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,AC=10,AA1=3,则球的体积的最大值为( )
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{9π}{2}$ |
6.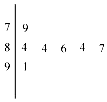 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
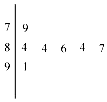 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,4 | D. | 85,1.6 |
4.已知复数z=a+i,a∈R,若z+$\overline{z}$=2,则复数z的共轭复数$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |