题目内容
分析方程sinx-cos2x+a=0在x∈[0,2π)的解的个数.
考点:根的存在性及根的个数判断
专题:三角函数的求值
分析:首先根据sinx-cos2x+a=0,可得a=-sinx+cos2x=
-(sinx+
)2,令f(x)=
-(sinx+
)2;然后画出函数f(x)=
-(sinx+
)2的图象,最后根据a的取值判断函数与直线的公共点的情况,进而判断出方程sinx-cos2x+a=0在x∈[0,2π)的解的个数即可.
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
解答:
解:根据sinx-cos2x+a=0,
可得a=-sinx+cos2x=
-(sinx+
)2,
令f(x)=
-(sinx+
)2,画出函数f(x)=
-(sinx+
)2的图象如下:
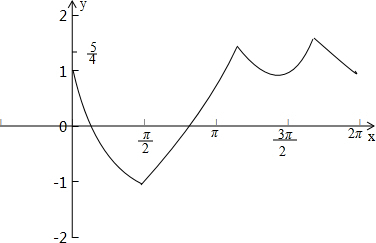
①a<-1或a>
时,方程无解;
②a=-1时,方程有1个解;
③-1<a<-1或a=
时,方程有2个解;
④1≤a<
时,方程有4个解.
可得a=-sinx+cos2x=
| 5 |
| 4 |
| 1 |
| 2 |
令f(x)=
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |

①a<-1或a>
| 5 |
| 4 |
②a=-1时,方程有1个解;
③-1<a<-1或a=
| 5 |
| 4 |
④1≤a<
| 5 |
| 4 |
点评:本题主要考查了根的存在性以及根的个数判断,以及函数的图象和性质,还考查了数形结合法的运用,属于中档题,数形结合是数学解题中常用的思想方法,它能使使复杂的问题简单化.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,目标函数z=mx+y仅在点(0,1)处取得最小值,则m的取值范围是( )
|
| A、(-∞,4 |
| B、(4,+∞) |
| C、(-∞,1) |
| D、(1,+∞) |
 已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.
已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.