题目内容
 已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.
已知多面体ABCDFE中,四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD,O、M分别为AB、FC的中点,且AB=2,AD=EF=1.(Ⅰ)求证:AF⊥平面FBC;
(Ⅱ)求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD:VF-CBE的值.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:
分析:(Ⅰ)欲证AF⊥平面FBC,根据直线与平面垂直的判定定理可知只需证AF与平面FBC内两相交直线垂直,而BC⊥AF,BF⊥AF,BC∩BF=B,满足定理条件;
(Ⅱ)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可,取FD中点N,连接MN、AN,易得OM∥ON,找出了定理的条件;
(Ⅲ)过F作FG⊥AB与G,由题意可得:FG⊥平面ABCD,求出VF-ABCD=
FG,VF-CBE=VC-BFE=
FG,即可得出结论.
(Ⅱ)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM与平面DAF内一直线平行即可,取FD中点N,连接MN、AN,易得OM∥ON,找出了定理的条件;
(Ⅲ)过F作FG⊥AB与G,由题意可得:FG⊥平面ABCD,求出VF-ABCD=
| 2 |
| 3 |
| 1 |
| 6 |
解答:
(Ⅰ)证明:∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB
BC?平面ABCD,而四边形ABCD为矩形∴BC⊥AB,
∴BC⊥平面ABEF∵AF?平面ABEF∴BC⊥AF
∵BF⊥AF,BC∩BF=B∴AF⊥平面FBC;
(Ⅱ)证明:取FD中点N,连接MN、AN,则MN∥CD,且MN=
CD,
又四边形ABCD为矩形,∴MN∥OA,且MN=OA
∴四边形AOMN为平行四边形,∴OM∥AN
又∵OM?平面DAF,AN?平面DAF∴OM∥平面DAF. …(8分)
(Ⅲ)解:过F作FG⊥AB与G,由题意可得:FG⊥平面ABCD
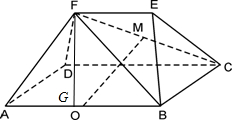
∴VF-ABCD=
S矩形ABCD×FG=
FG
∵CB⊥平面ABEF,
∴VF-CBE=VC-BFE=
S△BFE×CB=
•
EF•FG•CB=
FG,
∴VF-ABCD:VF-CBE=4:1 …(12分)
BC?平面ABCD,而四边形ABCD为矩形∴BC⊥AB,
∴BC⊥平面ABEF∵AF?平面ABEF∴BC⊥AF
∵BF⊥AF,BC∩BF=B∴AF⊥平面FBC;
(Ⅱ)证明:取FD中点N,连接MN、AN,则MN∥CD,且MN=
| 1 |
| 2 |
又四边形ABCD为矩形,∴MN∥OA,且MN=OA
∴四边形AOMN为平行四边形,∴OM∥AN
又∵OM?平面DAF,AN?平面DAF∴OM∥平面DAF. …(8分)
(Ⅲ)解:过F作FG⊥AB与G,由题意可得:FG⊥平面ABCD

∴VF-ABCD=
| 1 |
| 3 |
| 2 |
| 3 |
∵CB⊥平面ABEF,
∴VF-CBE=VC-BFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴VF-ABCD:VF-CBE=4:1 …(12分)
点评:本题主要考查了直线与平面垂直、直线与平面平行的判定,考查体积的计算考查空间想象能力、运算求解能力、推理论证能力,考查数形结合思想.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 如图是某几何体的三视图
如图是某几何体的三视图