题目内容
某种灯泡使用寿命在1000小时以上的概率为0.2，则三个这样的灯泡使用1000小时后，至多只坏一个的概率是 ．
考点：互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：题意知3个相互独立的灯泡使用的时间能否超过1000小时，可以看做一个做了3次独立重复试验的概率，根据独立重复试验的公式得到结果．
解答：
解：∵灯泡的耐用时间超过1000小时的概率为0.2，
3个相互独立的灯泡使用的时间能否超过1000小时，
可以看做一个做了3次独立重复试验的概率，
∴最多只有1个损坏的概率是0.23+C31×0.8×0.22=0.096+0.008=0.104
故答案为：0.104
3个相互独立的灯泡使用的时间能否超过1000小时，
可以看做一个做了3次独立重复试验的概率，
∴最多只有1个损坏的概率是0.23+C31×0.8×0.22=0.096+0.008=0.104
故答案为：0.104
点评：本题考查n次独立重复试验中恰好发生k次的概率，本题解题的关键是看出本试验符合独立重复试验，本题是一个基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
将函数y=cos(2x-
)的图象向左平移
个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得函数图象的一条对称轴是（ ）
| π |
| 3 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
D、x=
|
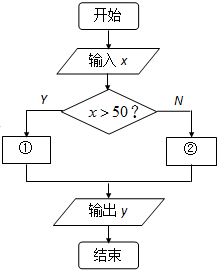某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为：不超过50kg按0.53元/kg收费，超过50kg的部分按0.85元/kg收费．相应收费系统的流程图如右图所示，则①处应填（ ）| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+（x-50）×0.85 |
| D、y=50×0.53+0.85x |
