题目内容
函数f(x)=
(x≤-1)的反函数为: .
| x2+x |
考点:反函数
专题:函数的性质及应用
分析:本题通过解方程的方法,用y表示x,得到原函数的反函数,得到本题结论.
解答:
解:∵函数f(x)=
(x≤-1),
∴y=
,
∴y2=x2+x,
∴x2+x-y2=0,
由求根公式可知:
x=
,
∵x≤-1,
∴x=
,
将“y”与“x”对调,得到:
y=-
-
(x≥0).
∴函数f(x)=
(x≤-1)的反函数为y=-
-
(x≥0).
故答案为:y=-
-
(x≥0).
| x2+x |
∴y=
| x2+x |
∴y2=x2+x,
∴x2+x-y2=0,
由求根公式可知:
x=
-1±
| ||
| 2 |
∵x≤-1,
∴x=
-1-
| ||
| 2 |
将“y”与“x”对调,得到:
y=-
| 1 |
| 2 |
x2+
|
∴函数f(x)=
| x2+x |
| 1 |
| 2 |
x2+
|
故答案为:y=-
| 1 |
| 2 |
x2+
|
点评:本题考查了反函数的求法,本题难度不大,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
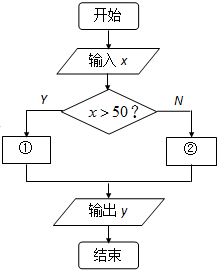 某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )
某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+(x-50)×0.85 |
| D、y=50×0.53+0.85x |
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第202次互换座位后,小兔坐在第( )号座位上
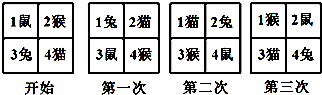

| A、1 | B、2 | C、3 | D、4 |
若在区间[0,2]中随机地取两个数,则这两个数中较小的数大于
的概率是( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设全集U=R,集合A={x|x<0},B={x|-1<x<3},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x<0} |
| D、{x|x<3} |