题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2B=sinAsinC.
(Ⅰ)求ac-b2的值;
(Ⅱ)若b=
,且
•
=
,求|
+
|的值.
(Ⅰ)求ac-b2的值;
(Ⅱ)若b=
| 2 |
| BA |
| BC |
| 3 |
| 2 |
| BC |
| BA |
考点:平面向量数量积的运算,正弦定理
专题:平面向量及应用
分析:(Ⅰ)首先利用正弦定理把三角函数中角的关系式转化成边的关系式,直接求出结果.
(Ⅱ)利用余弦定理求出a2+c2=5,在用向量的数量积和向量的模求出结果.
(Ⅱ)利用余弦定理求出a2+c2=5,在用向量的数量积和向量的模求出结果.
解答:
解:(Ⅰ)因为sin2B=sinA•sinC,
由正弦定理得b2=ac,所以ac-b2=0
(Ⅱ)因为b2=ac,b=
,所以b2=2,ac=2
所以
•
=cacosB=
,
由余弦定理得a∈R,所以b2=a2+c2-2accosB.
所以a2+c2=5,
|
+
|2=a2+c2+2accosB=8,
|
+
|=2
.
由正弦定理得b2=ac,所以ac-b2=0
(Ⅱ)因为b2=ac,b=
| 2 |
所以
| BA |
| BC |
| 3 |
| 2 |
由余弦定理得a∈R,所以b2=a2+c2-2accosB.
所以a2+c2=5,
|
| BC |
| BA |
|
| BC |
| BA |
| 2 |
点评:本题考查的知识要点:正弦定理和余弦定理得应用,向量的数量积和向量的模的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图是正方体的平面展开图,则在这个正方体中:
如图是正方体的平面展开图,则在这个正方体中:①BM与ED平行②CN与BE是异面直线
③CN与BM成60°角④DM与BN是异面直线
以上四个命题中,正确的命题序号是( )
| A、①②③ | B、②④ |
| C、③④ | D、②③④ |
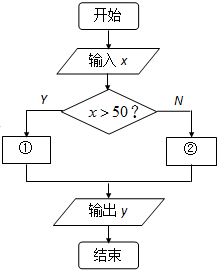 某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )
某铁路客运部门规定甲、乙两地之间旅客托运行李的费用为:不超过50kg按0.53元/kg收费,超过50kg的部分按0.85元/kg收费.相应收费系统的流程图如右图所示,则①处应填( )| A、y=0.85x |
| B、y=0.53x |
| C、y=50×0.53+(x-50)×0.85 |
| D、y=50×0.53+0.85x |