题目内容
2．x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$，若z=y-ax取得最大值的最优解不唯一，则实数a的值为（ ）| A． | $\frac{1}{2}$或-1 | B． | 2或$\frac{1}{2}$ | C． | 2或-1 | D． | 2或1 |
分析 由题意作出已知条件的平面区域，将z=y-ax化为y=ax+z，z相当于直线y=ax+z的纵截距，由几何意义可得．
解答 解：由题意作出约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$，平面区域，
将z=y-ax化为y=ax+z，z相当于直线y=ax+z的纵截距，
由题意可得，y=ax+z与y=2x+2或与y=2-x平行，
故a=2或-1；
故选：C．
点评 本题考查了简单线性规划，作图要细致认真，注意目标函数的几何意义是解题的关键之一，属于中档题．
练习册系列答案
相关题目
12．复数$z=\frac{4}{1+i}$（i是虚数单位）的共轭复数在复平面内对应的点是（ ）
| A． | （2，-2） | B． | （2，2） | C． | （-2，-2） | D． | （-2，2） |
13．
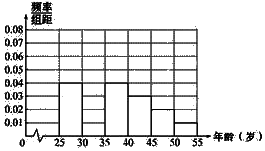我校高二同学利用暑假进行了社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
（1）请你补全频率分布直方图，并求出n，a，p的值；
（2）请你利用频率分布直方图估计本次调查人群的年龄的中位数．
我校高二同学利用暑假进行了社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：| 组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25，30） | 120 | 0.6 |
| 第二组 | [30，35） | 195 | p |
| 第三组 | [35，40） | 100 | 0.5 |
| 第四组 | [40，45） | a | 0.4 |
| 第五组 | [45，50） | 30 | 0.3 |
| 第六组 | [50，55] | 15 | 0.3 |
（2）请你利用频率分布直方图估计本次调查人群的年龄的中位数．