题目内容
数列{bn}满足:bn+1=2bn+2,bn=an+1-an,且a1=2,a2=4.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)求数列{an的前n项和Sn.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)求数列{an的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出数列{bn+2}是首项为4,公比为2的等比数列,由此能求出bn=2n+1-2.
(Ⅱ)由an-an-1=bn=2n-2,n≥2,得an-an-1=2n-2,n≥2,由此累加得an=2n+1-2n,由此能求出数列{an的前n项和Sn.
(Ⅱ)由an-an-1=bn=2n-2,n≥2,得an-an-1=2n-2,n≥2,由此累加得an=2n+1-2n,由此能求出数列{an的前n项和Sn.
解答:
解:(Ⅰ)∵bn+1=2bn+2,
∴bn+1+2=2(bn+2),
∴
=2,
又b1+2=a2-a1+2=4,
∴数列{bn+2}是首项为4,公比为2的等比数列.
即bn+2=4•2n-1=2n+1,
所以bn=2n+1-2.…(6分)
(Ⅱ)由(Ⅰ)知:an-an-1=bn=2n-2,n≥2,
∴an-an-1=2n-2,n≥2,
令n=2,3,4,…,n-1,
赋值累加得an-2=(22+23+…+2n)-2(n-1),
∴an=(2+22+23+…+2n)-2n+2
=
-2n+2
=2n+1-2n,
∴Sn=
-
=2n+2-(n2+n+4).…(12分)
∴bn+1+2=2(bn+2),
∴
| bn+1+2 |
| bn+2 |
又b1+2=a2-a1+2=4,
∴数列{bn+2}是首项为4,公比为2的等比数列.
即bn+2=4•2n-1=2n+1,
所以bn=2n+1-2.…(6分)
(Ⅱ)由(Ⅰ)知:an-an-1=bn=2n-2,n≥2,
∴an-an-1=2n-2,n≥2,
令n=2,3,4,…,n-1,
赋值累加得an-2=(22+23+…+2n)-2(n-1),
∴an=(2+22+23+…+2n)-2n+2
=
| 2(2n-1) |
| 2-1 |
=2n+1-2n,
∴Sn=
| 4(1-2n) |
| 1-2 |
| n(2+2n) |
| 2 |
=2n+2-(n2+n+4).…(12分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意累加法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数x、y满足不等式组
,则3x+y的取值范围为( )
|
A、[-3,-
| ||||
B、[-3,-
| ||||
C、[-
| ||||
D、[-
|
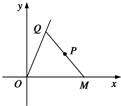 有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
有定点P(6,4)及定直线l:y=4x,点Q是l上在第一象限内的点,PQ交x轴的正半轴于点M,
