题目内容
方程log3x+x=3的解的个数是 ．
考点：根的存在性及根的个数判断
专题：数形结合,函数的性质及应用
分析：函数y=log3x，函数y=3-x，画出图象的看交点个数，可判断解的个数．
解答：
解：根据函数y=log3x，函数y=3-x，图象的交点个数可判断：方程log3x+x=3的解的个数是1，
故答案为：1
解：根据函数y=log3x，函数y=3-x，图象的交点个数可判断：方程log3x+x=3的解的个数是1，故答案为：1
点评：本题考察了运用函数图象的交点，判断方程根的个数，属于中档题．
练习册系列答案
相关题目
动点P到点A（8，0）的距离是到点B（2，0）的距离的2倍，则动点P的轨迹方程为（ ）
| A、x2+y2=32 |
| B、x2+y2=16 |
| C、（x-1）2+y2=16 |
| D、x2+（y-1）2=16 |
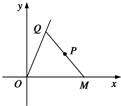有定点P（6，4）及定直线l：y=4x，点Q是l上在第一象限内的点，PQ交x轴的正半轴于点M，
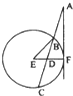如图，过圆E外一点A作一条直线与圆E交与B，且AB=设α是第二象限角，P（x，4）为其终边上的一点，且cosα=
x，则tanα等于（ ）
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|