题目内容
已知函数f(x)=2cos2x+2asinxcosx-1的图象关于直线x=
对称.
(Ⅰ)求a的值;
(Ⅱ)把函数y=f(x)的图象向右平移k(k>0)个单位后与函数g(x)=
sin2x的图象重合,求k的最小值.
| π |
| 8 |
(Ⅰ)求a的值;
(Ⅱ)把函数y=f(x)的图象向右平移k(k>0)个单位后与函数g(x)=
| 2 |
考点:两角和与差的正弦函数,正弦函数的对称性,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:(Ⅰ)根据函数f(x)=2cos2x+2asinxcosx-1的图象关于直线x=
对称,可得f(0)=f(
),即可求a的值;
(II)先化简函数,再按照图象平移的规律,利用把函数y=f(x)的图象向右平移k(k>0)个单位后与函数g(x)=
sin2x的图象重合,即可求k的最小值.
| π |
| 8 |
| π |
| 4 |
(II)先化简函数,再按照图象平移的规律,利用把函数y=f(x)的图象向右平移k(k>0)个单位后与函数g(x)=
| 2 |
解答:
解:(Ⅰ)∵函数f(x)=2cos2x+2asinxcosx-1的图象关于直线x=
对称,
∴f(0)=f(
),
∴2-1=1+a-1,∴a=1;
(Ⅱ)f(x)=2cos2x+2asinxcosx-1=cos2x+sin2x=
sin(2x+
),
函数y=f(x)的图象向右平移k(k>0)个单位后,得到g(x)=
sin[2(x-k)+
)]=
sin(2x-2k+
)=
sin2x,
∴k的最小值为
.
| π |
| 8 |
∴f(0)=f(
| π |
| 4 |
∴2-1=1+a-1,∴a=1;
(Ⅱ)f(x)=2cos2x+2asinxcosx-1=cos2x+sin2x=
| 2 |
| π |
| 4 |
函数y=f(x)的图象向右平移k(k>0)个单位后,得到g(x)=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
∴k的最小值为
| π |
| 8 |
点评:解决三角函数的性质问题,应该先利用三角函数的公式化简三角函数为一个角一个函数的形式;图象的平移遵循左加右减上原则.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
线性回归方程表示的直线
=a+bx,必定过( )
 |
| y |
| A、(0,0)点 | ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
直线x+y=0与圆(x-2)2+y2=4相交所得线段的长度为( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
在△ABC中,角A、B、C所对的边分别为a、b、c,若acosB+bcosA=csinC且a=b,则角B等于( )
| A、30° | B、45° |
| C、60° | D、90° |
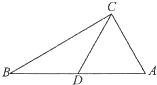 如图在△ABC中,已知∠A=
如图在△ABC中,已知∠A=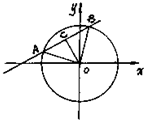 已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.