题目内容
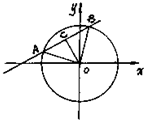 已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
考点:直线和圆的方程的应用,基本不等式在最值问题中的应用
专题:直线与圆
分析:(1)求出圆心到直线的距离OC,求出弦长AB,由三角形的面积公式即可求出面积S(k),并写出定义域;
(2)分子、分母同除以|k|,然后对分母应用基本不等式,求出最小值,注意等号成立的条件,从而得到S的最大值.
(2)分子、分母同除以|k|,然后对分母应用基本不等式,求出最小值,注意等号成立的条件,从而得到S的最大值.
解答:
解:(1)过O作OC⊥AB,垂足为C,则C为AB的中点,
又OC=
,AB=2
=2
=
,
 ∴S(k)=
∴S(k)=
•OC•AB=
,定义域为{k|k∈R且k≠0};
(2)∵S=
,
∴S=
,
∵|k|+
≥2,
∴S≤
=2,
∴当且仅当|k|=
即k=±1时,S取最大值,且为2.
又OC=
| |2k| | ||
|
| 4-OC2 |
4-
|
| 4 | ||
|
 ∴S(k)=
∴S(k)=| 1 |
| 2 |
| 4|k| |
| 1+k2 |
(2)∵S=
| 4|k| |
| 1+k2 |
∴S=
| 4 | ||
|k|+
|
∵|k|+
| 1 |
| |k| |
∴S≤
| 4 |
| 2 |
∴当且仅当|k|=
| 1 |
| |k| |
点评:本题主要考查直线与圆的位置关系:相交,考查弦长的求法,考查基本不等式及应用于求最值,注意等号成立的条件.

练习册系列答案
相关题目
若数列{n(n+4)(
)n}中的最大项是第k项,则k=( )
| 2 |
| 3 |
| A、4 | B、5 | C、6 | D、7 |