题目内容
若数列{an}是首项为
，公比为
的等比数列，数列{bn}满足bn=log2
，则数列{anbn}的前n项和是 ．
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| an |
考点：数列的求和,等差数列的性质
专题：计算题,等差数列与等比数列
分析：求出数列{an}、数列{bn}的通项公式代入anbn，利用错位相减法求得其前n项和Sn．
解答：
解：∵数列{an}是首项为
，公比为
的等比数列，
∴an=
，
∴bn=log2
=n，
∴anbn=n•
，
∴Sn=1•2+2•22+3•23++（n-1）•2n-1+n•2n．①
2Sn=1•22+2•23++（n-1）•2n+n•2n+1．②
①-②得-Sn=1•2+22+23++2n-n•2n+1=
-n•2n+1．
∴Sn=2-2n+1+n•2n+1．
故答案为：2-2n+1+n•2n+1．
| 1 |
| 2 |
| 1 |
| 2 |
∴an=
| 1 |
| 2n |
∴bn=log2
| 1 |
| an |
∴anbn=n•
| 1 |
| 2n |
∴Sn=1•2+2•22+3•23++（n-1）•2n-1+n•2n．①
2Sn=1•22+2•23++（n-1）•2n+n•2n+1．②
①-②得-Sn=1•2+22+23++2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Sn=2-2n+1+n•2n+1．
故答案为：2-2n+1+n•2n+1．
点评：考查等差数列和等比数列的通项公式、错位相减法求数列的前项和Sn，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，角A，B，C的对边分别为a，b，c，若a2-b2=
bc，且sinC=2
sinB，则A等于（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
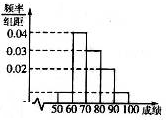某校200名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100）．则成绩在[90，100]内的人数为（ ）