题目内容
7.已知双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),则其渐近线的方程为$y=±\sqrt{3}x$.分析 利用双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),求出b,即可求出双曲线渐近线的方程.
解答 解:∵双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),
∴1+b2=4,
∵b>0,
∴b=$\sqrt{3}$,
又a=1,∴双曲线渐近线的方程为$y=±\sqrt{3}x$
故答案为:$y=±\sqrt{3}x$.
点评 本题考查双曲线渐近线的方程,考查学生的计算能力,正确求出b是关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
17.已知定义在R上的函数f(x)=x2+|x-m|(m为实数)是偶函数,记a=f(log${\;}_{\frac{1}{3}}$e),b=f(log3π),c=f(em)(e为自然对数的底数),则a,b,c的大小关系( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
18.若曲线y2=2px(p>0)上只有一个点到其焦点的距离为1,则p的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.已知集合M={1,2,3},N={2,3,4,5},那么M∩N=( )
| A. | ∅ | B. | {1,4,5} | C. | {1,2,3,4,5} | D. | {2,3} |
17.已知动圆M与y轴相切且与定圆A:(x-3)2+y2=9外切,则动圆的圆心M的轨迹方程是( )
| A. | y2=12x(x>0) | B. | y=0(x<0) | ||
| C. | y2=12x | D. | y2=12x(x>0)或y=0(x<0) |
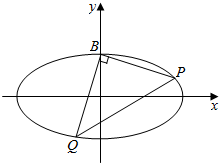 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,一个顶点是B(0,1).