题目内容
19.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,点$A(1,\frac{{\sqrt{3}}}{2})$在椭圆C上,O为坐标原点.(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线l与椭圆C有且仅有一个公共点,且l与圆x2+y2=5的相交于不在坐标轴上的两点P1,P2,记直线OP1,OP2的斜率分别为k1,k2,求证:k1•k2为定值.
分析 (Ⅰ)利用离心率列出方程,通过点在椭圆上列出方程,求出a,b然后求出椭圆的方程.
(Ⅱ)当直线l的斜率不存在时,验证直线OP1,OP2的斜率之积.
当直线l的斜率存在时,设l的方程为y=kx+m与椭圆联立,利用直线l与椭圆C有且只有一个公共点,推出m2=4k2+1,通过$\left\{\begin{array}{l}y=kx+m\\{x^2}+{y^2}=5\end{array}\right.$,设P1(x1,y1),P2(x2,y2),结合韦达定理,求解直线的斜率乘积,推出k1•k2为定值即可.
解答 (本小题满分14分)
(Ⅰ)解:由题意,得$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,a2=b2+c2,…(2分)
又因为点$A(1,\frac{{\sqrt{3}}}{2})$在椭圆C上,
所以$\frac{1}{a^2}+\frac{3}{{4{b^2}}}=1$,…(3分)
解得a=2,b=1,$c=\sqrt{3}$,
所以椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$.…(5分)
(Ⅱ)证明:当直线l的斜率不存在时,由题意知l的方程为x=±2,
易得直线OP1,OP2的斜率之积${k_1}•{k_2}=-\frac{1}{4}$.…(6分)
当直线l的斜率存在时,设l的方程为y=kx+m.…(7分)
由方程组$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$得(4k2+1)x2+8kmx+4m2-4=0,…(8分)
因为直线l与椭圆C有且只有一个公共点,
所以△=(8km)2-4(4k2+1)(4m2-4)=0,即m2=4k2+1.…(9分)
由方程组$\left\{\begin{array}{l}y=kx+m\\{x^2}+{y^2}=5\end{array}\right.$得(k2+1)x2+2kmx+m2-5=0,…(10分)
设P1(x1,y1),P2(x2,y2),则${x_1}+{x_2}=\frac{-2km}{{{k^2}+1}}$,${x_1}•{x_2}=\frac{{{m^2}-5}}{{{k^2}+1}}$,…(11分)
所以${k_1}•{k_2}=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{(k{x_1}+m)(k{x_2}+m)}}{{{x_1}{x_2}}}=\frac{{{k^2}{x_1}{x_2}+km({x_1}+{x_2})+{m^2}}}{{{x_1}{x_2}}}$=$\frac{{{k^2}•\frac{{{m^2}-5}}{{{k^2}+1}}+km•\frac{-2km}{{{k^2}+1}}+{m^2}}}{{\frac{{{m^2}-5}}{{{k^2}+1}}}}=\frac{{{m^2}-5{k^2}}}{{{m^2}-5}}$,…(13分)
将m2=4k2+1代入上式,
得${k_1}•{k_2}=\frac{{-{k^2}+1}}{{4{k^2}-4}}=-\frac{1}{4}$.
综上,k1•k2为定值$-\frac{1}{4}$.…(14分)
点评 本题考查椭圆的标准方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | (x-1)2+y2=1 | B. | x2+(y+1)2=1 | C. | x2+(y-1)2=1 | D. | (x+1)2+y2=1 |
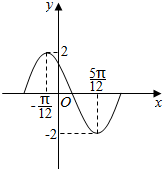 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).