题目内容
2.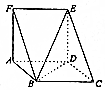 如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.
如图,三棱柱ABF-DCE中,∠ABC=120°,BC=2CD,AD=AF,AF⊥平面ABCD.(Ⅰ)求证:BD⊥EC;
(Ⅱ)若AB=1,求四棱锥B-ADEF的体积.
分析 (Ⅰ)证明ED⊥BD,BD⊥CD.推出BD⊥平面ECD.然后证明BD⊥EC;
(Ⅱ)作BH⊥AD于H,求出高BH=$\frac{\sqrt{3}}{2}$,然后求解几何体的体积.
解答 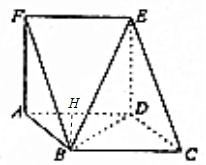 (Ⅰ)证明:三棱柱ABF-DCE中,AF⊥平面ABCD.∴DE∥AF,ED⊥平面ABCD,
(Ⅰ)证明:三棱柱ABF-DCE中,AF⊥平面ABCD.∴DE∥AF,ED⊥平面ABCD,
∵BD?平面ABCD,∴ED⊥BD,
又ABCD是平行四边形,∠ABC=120°,故∠BCD=60°.
∵BC=2CD,故∠BDC=90°.故BD⊥CD.
∵ED∩CD=D,∴BD⊥平面ECD.
∵EC?平面ECD,
∴BD⊥EC;
(Ⅱ)解:由BC=2CD,可得AD=2AB,∵AB=1,∴AD=2,作BH⊥AD于H,
∵AF⊥平面ABCD,∴BH⊥平面ADEF,又∠ABC=120°,
∴BH=$\frac{\sqrt{3}}{2}$,
∴${V}_{B-ADEF}=\frac{1}{3}×(2×2)×\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体四棱锥B-ADEF的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
12.执行如图所示的程序框图,则输出的结果为( )


| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
13.已知复数z满足z($\sqrt{7}$+3i)=16i(i为虚数单位),则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 4 | D. | 8 |
7.若a=($\frac{1}{2}$)10,b=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,c=log${\;}_{\frac{1}{3}}$10,则a,b.c大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>a>c |
11.对于两条不同的直线m,n和两个不同的平面α,β,以下结论正确的是( )
| A. | 若m?α,n∥β,m,n是异面直线,则α,β相交 | |
| B. | 若m⊥α,m⊥β,n∥α,则n∥β | |
| C. | 若m?α,n∥α,m,n共面于β,则m∥n | |
| D. | 若m⊥α,n⊥β,α,β不平行,则m,n为异面直线 |
12.已知集合A={x|0≤x≤5},B={x∈N*|x-1≤2}则A∩B=( )
| A. | {x|1≤x≤3} | B. | {x|0≤x≤3} | C. | {1,2,3} | D. | {0,1,2,3} |